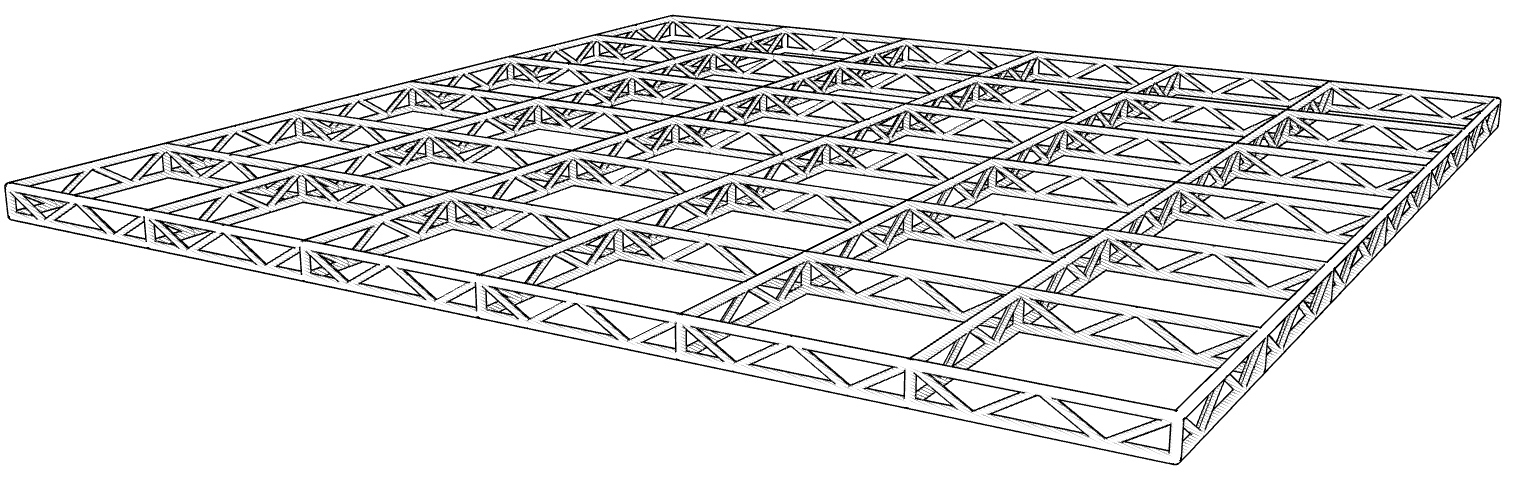
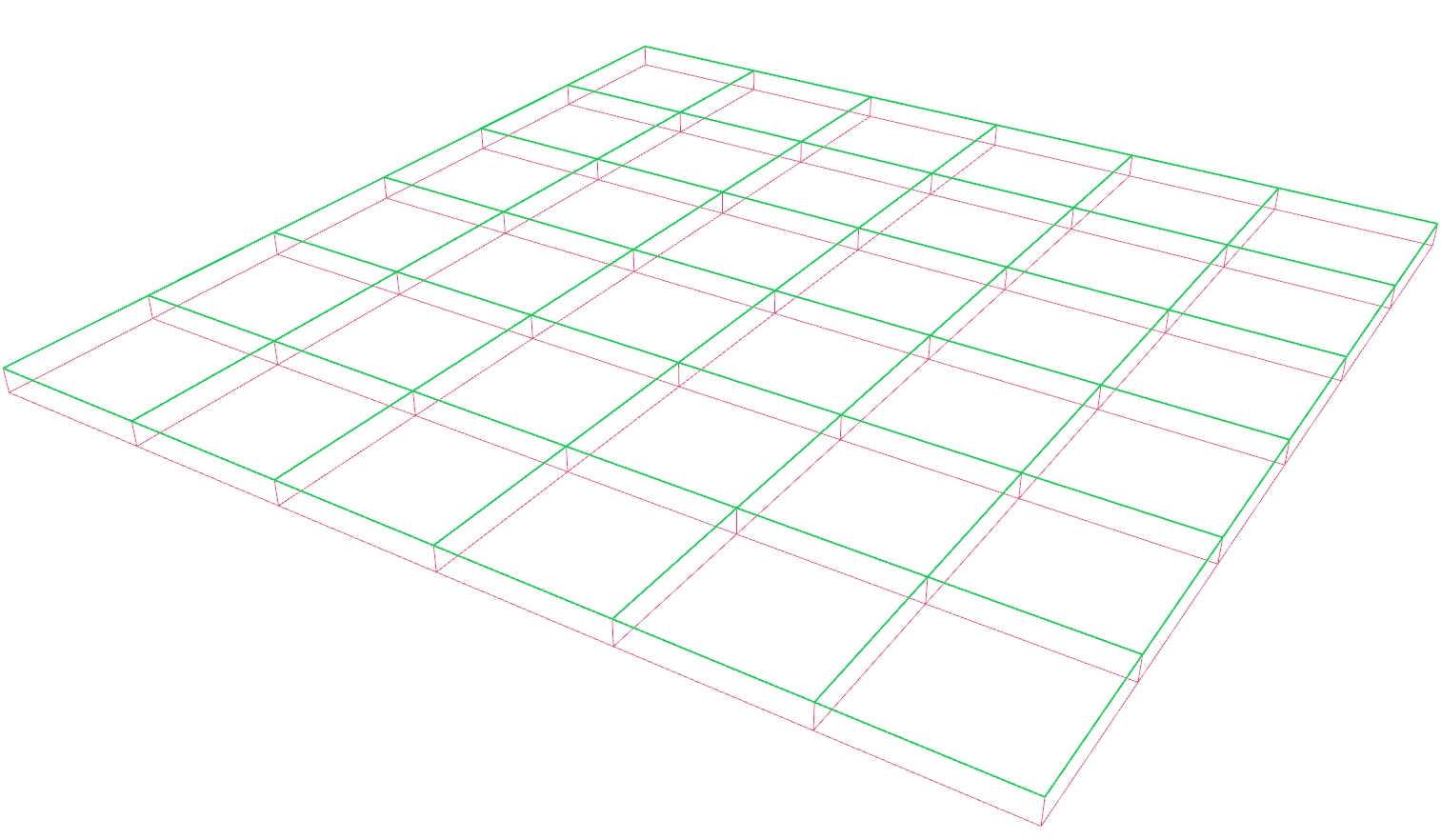
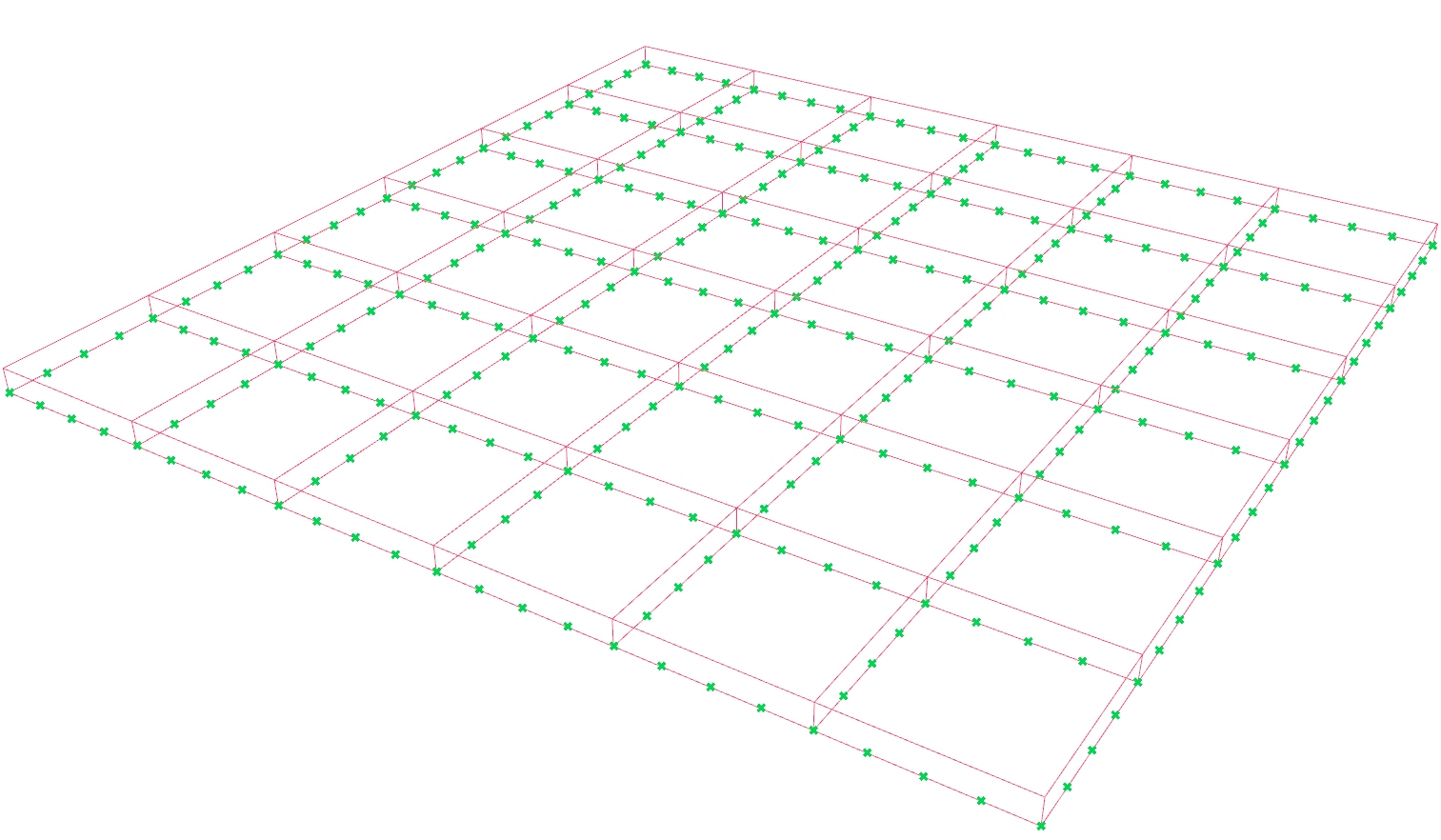
In this tutorial, we will create a truss grid. For this, we need a basic grid pattern and trussed girders along the axes of the grid. Meanwhile, we learn common operations with data trees.

Grasshopper

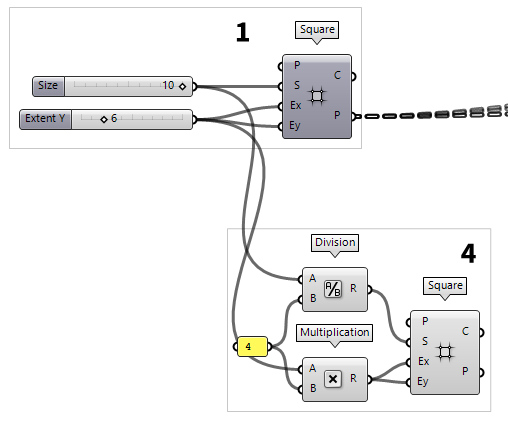
1

Generate a basic grid pattern

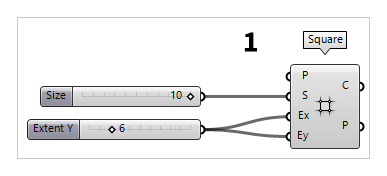
First thing to do, is to create the basic grid. For this, we use a Squarecomponent and, at the moment, we are interested in the inputs S (Size), Ex (Extent X), and Ey (Extent Y). By connecting a Number Sliders to these inputs, we can dynamically control the size and extend of the square grid.

Show Rhino Show Grasshopper

2

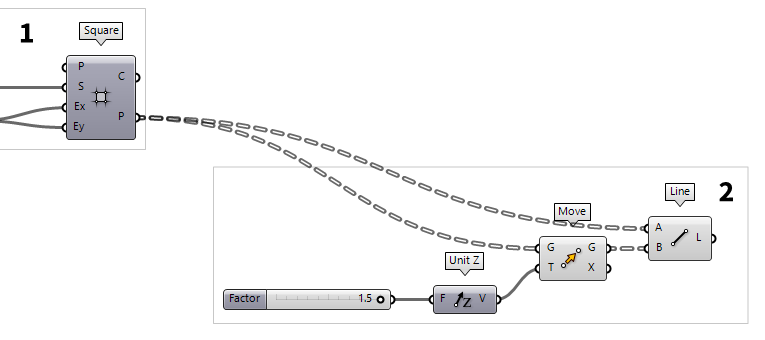
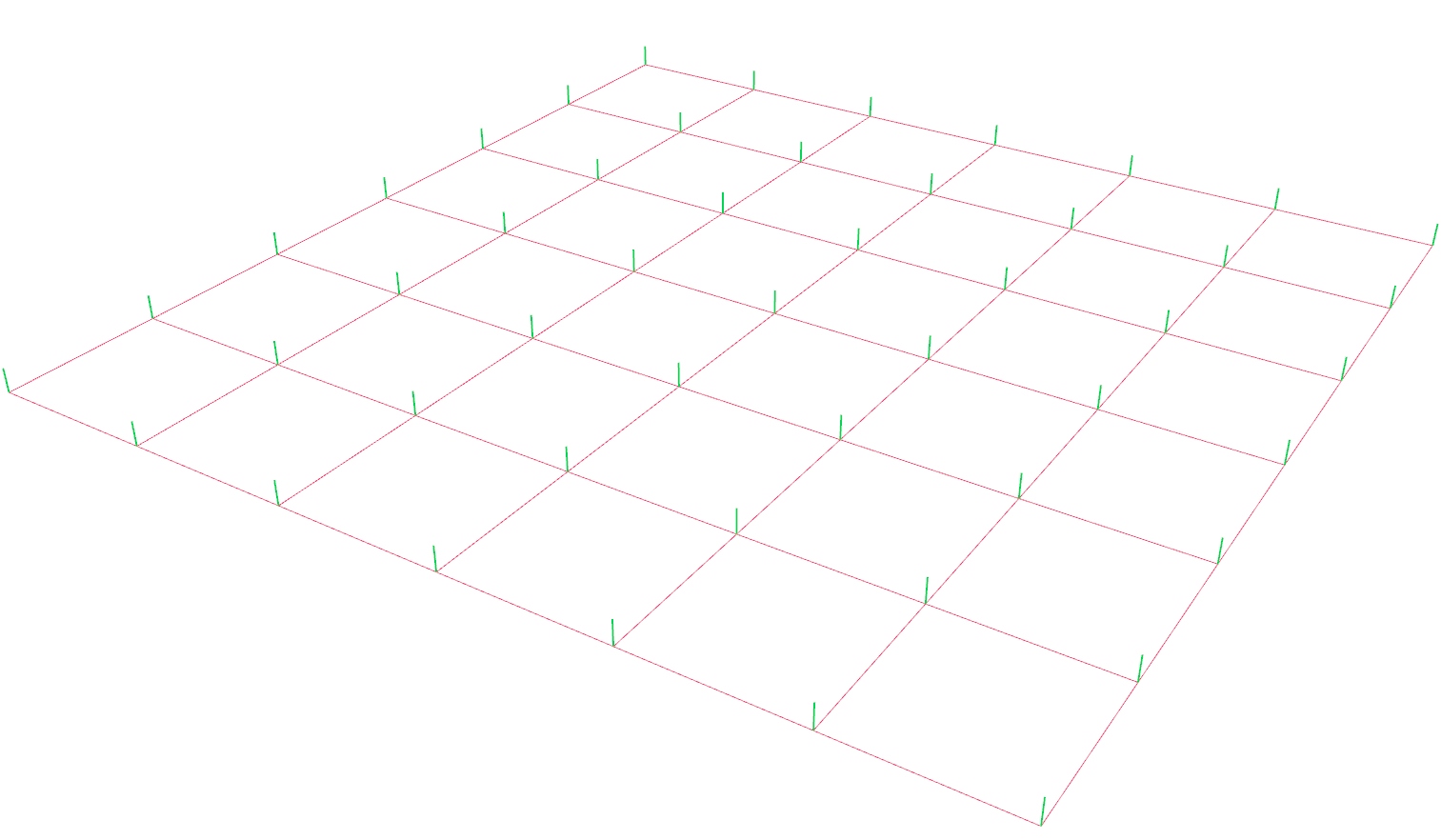
Create the vertical members

After generating the basic grid, we get its corner points at output P. To create the vertical members, we need to create a second set of points above our basic grid. For this, we use a Movecomponent and connect the corner points to its input G, which collects the geometry we want to move. Input T takes the translation vector.

The translation vector is defined with a Unit Zcomponent. This gives us the direction of the vector. To set the vector length, we adjust the unit multiplication factor at input F with another slider. After typing 0.5..1.5 into the Canvas Search, we get a Number Sliderwith once decimal ranging from 0.5 to 1.5. After wiring the components, we can now dynamically change the offset of the second set of points.

To create the vertical members, we use a Linecomponent and connect the points at ground level to input A and the moved points to input B.

Show Rhino Show Grasshopper

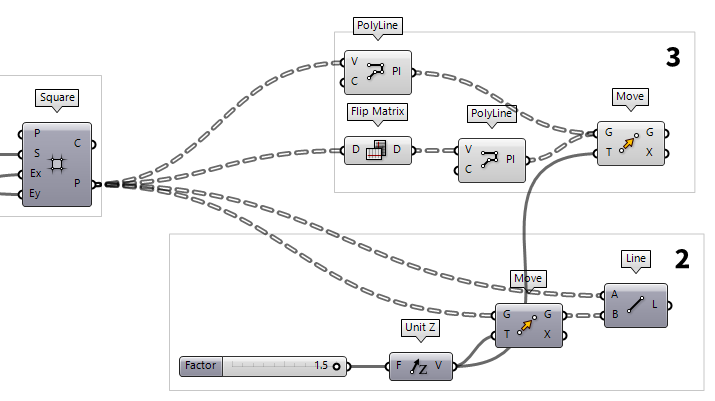
3

Create the upper and lower chords

At output P of the grid, the points at the grid corners are structured in a data tree format: each branch holds the points for one column. If we connect a PolyLinecomponent to these points, we get polylines in the column direction.

To create lines in the row direction, we need to change the structure of the data tree by using a Flip Matrixcomponent. Now each branch holds the points for one row. Thus, another PolyLinecomponent will create lines in the row direction.

The just created polylines represent the lower chords of our truss grid and we need another Movecomponent to create the upper chords. Because the geometry we feed into a Move component is still available in the component(s) before, we use Move for copying something (and there is no Copy component). We just need to remember that if we want to progress the chords, we have to connect wires to the outputs off all three components to grab all chords. We can connect two wires with input G by holding down Shift while connecting the wires. At input T we connect the translation vector from step 2.

Show Rhino Show Grasshopper

4

Generate a sub grid

The next thing we want to create are the diagonal members. Here, we don’t want the diagonals to run between the points from before, but in a zigzag with a higher frequency (as shown in the sketch).

To find the points for the higher frequency, we will use another Squaregrid with smaller cells. Because the sub grid is depending on the main grid, we have to use the initial sliders to keep the algorithm parametric. In this example, we will place four diagonals between the main grid corners. Therefore, we use a Divisioncomponent and connect the Size slider to input A. At input B we connect a Panelwith the value of 4. Now 4 cells of the sub grid span the distance of one cell from the main grid.

Because the cells of the sub grid are smaller, we need more of them to cover the area of the main grid: We use a Multiplicationcomponent and connect it to the Extend slider and also to the Panel with 4.

Show Rhino Show Grasshopper

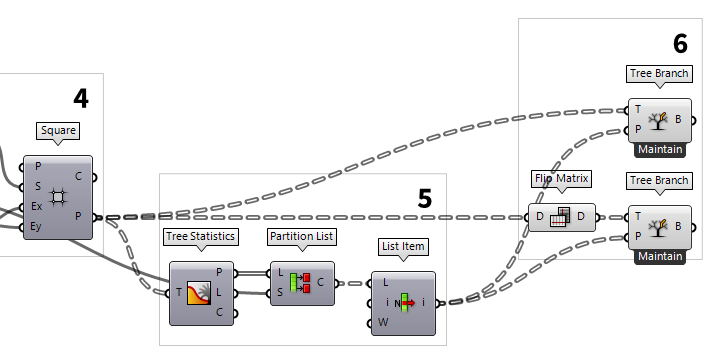
5

Identify the needed points from the sub grid

The output P returns all the points at the sub grid corners, however, we only need those that are on the axes of the main grid. We could either find them by analyzing their geometric location or by selecting the desired branches by name. In this example, we retrieve the points by doing the latter. To get the names of the branches, we hook up a Tree Statisticscomponent.

The names of the branches can be found at output P. Now, we need every fourth branch (or to be more precise, the first, then the fifth etc). To get every fourth name, we use a Partition Listcomponent and connect the names to input L and the panel with 4 to input S. This will chop the list of names into branches with four items each. Connecting a List Itemcomponent with default values will return the first item of each branch and those are the names we need.

6

Extract the needed sub points

Now that we have the names for the branches we want, we use a Tree Branchcomponent and connect the points to input T and the names to input P. This will select the columns of the sub grid that are on the main grid.

We also need the rows of the sub grid that are on the main grid. To get them, we need to use a Flip Matrixcomponent on the points before connecting them to another Tree Branchcomponent.

Show Rhino Show Grasshopper

7

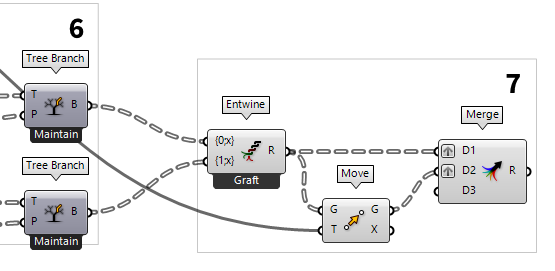
Move and pair the sub points

With the completion of step 6, we have the desired points from the sub grid. But, the column and row direction are separated in two components. We will now combine them into a single data tree, so that we can move the whole tree of points instead of two individual trees. To combine different trees into one tree, on which each branch contains an old tree, we will use the Entwinecomponents. However, the default settings don’t offer what we are looking for and therefore, we right-click the component and deselect Flatten Inputs.

After connecting each direction of points to its own input, we zoom in until we see the zoomable user interface and then press the little minus to remove the spare input. Now, we use another Movecomponent together with the translation vector from step 2 to create points on the upper chords.

Next, we want to combine the two sets of sub points into a data tree. But this time, we want branches that contain the two points that are on top of each other. Placing a Mergecomponent on the canvas and connecting the points from the upper and lower chords to it, will return lists of points that share the same column or row. To get the two opposing points in each list, we graft both inputs of Merge by right-clicking the input and selecting Graft. See essentials/data-trees#graftto learn how the data is restructured when grafting.

8

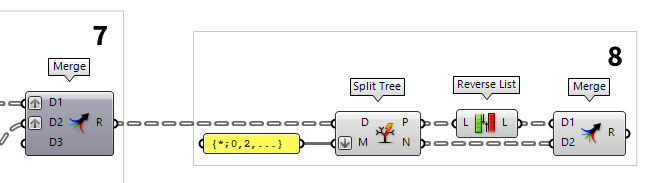
Flip every second pair of points

To run the zigzag for the diagonals, we will flip the order of every second pair of points. To select every second branch, we use a Split Treecomponent and connect the branches to input D. For input M, we create a Panelwith the content {*;0,2,...}. This pattern will select all branches that end with in even number. The how-to Split Treeexplains possible patterns in more detail. At output P we get the positive matches and at output N the negative ones.

To flip the order of the positive matches, we use a Reverse Listcomponent. Alternatively, we could right-click an input or output grip and select Reverse in the context menu. Then, we combine both lists with another Mergecomponent.

9

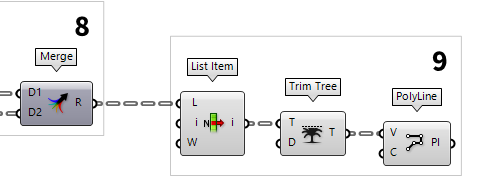
Create the diagonal members

After step 8, we have lists in which the first item is alternately on the lower and upper chord. Now, we will create a polyline that connects every first point. To grab the first item from a list, we use List Item. Now there is one item in each branch. To get all points in one column or row, we have to remove the last ramification with Trim Tree.

Finally, we connect a PolyLinecomponent to the output, which results in the generation of the diagonal members.

Show Rhino Show Grasshopper

Test your skills

Well, the above was certainly fun because the algorithm now includes all kinds of data tree operations, but of course, there is a quicker way, especially for creating the zigzag. We can, for example, not only use Split Treeto get every second path, but also every fifth one. Also, we can use specialized components to Merge lists more efficiently to get the points we need for the zigzag. A good place to start is after step 4.

Hint 1

Extract the needed sub points

As said, we can use Split Tree to select the branches we need from the sub gird. But, before we do that, we should use a Flip Matrixcomponent to also get the other direction. Then we combine both trees into one with Entwine(right-click to deselect Flatten Inputs).

Then we can use the Split Treecomponent and set the pattern to {*;0,4,...}, which selects every fifth branch from the sub grid. Using Movewith the translation vector from step 2 will create the second layer of points. Now we can mix and match them to create the zigzag. Just remember: each branch that we connect to the PolyLinecomponent to create the diagonals needs to have the same amount of points as after Split Tree.

Hint 2

Combine the points

There are different ways to combine the points for creating the diagonal members. You can do it either way.

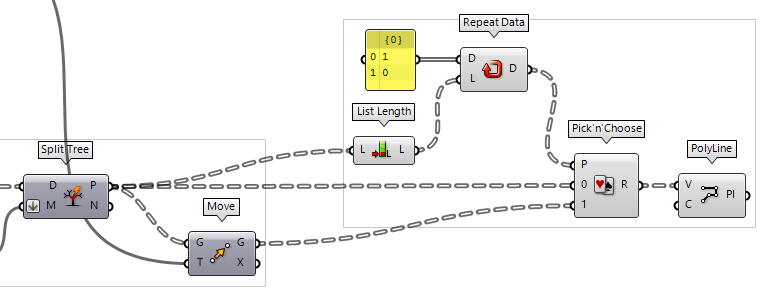
Pick’n’Choose

We could use Pick'n'Chooseand connect the lower points to one input and the upper points to another. Then, we also need a pattern which picks points alternately. The pattern is defined in a Panelwith two items; 1 and 0 (make sure to untoggle Multiline Data in the context menu of the panel).

Pick’n’Choose will not repeat the pattern internally and thus, we have to add a Repeat Datacomponent. The length of the pattern is given by the amount of points we have on one chord. This number can be retrieved with List Length.

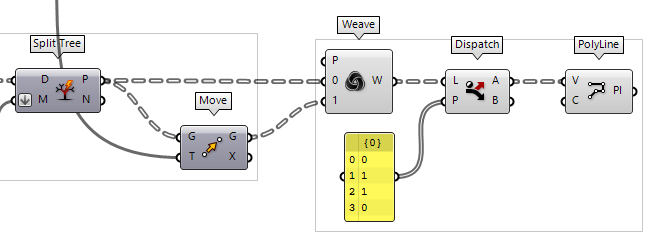
Weave and Dispatch

We could also use the Weavecomponent and connect each set of chords to one input. Weave will create a list with twice the amount of points needed, placing the points from the lower and upper chords alternately: First point from the lower chord, opposing point on the upper chord, second point from the lower chord, opposing point on the upper chords, and so forth.

Given this pattern, we just need to grab the desired points, which we do with a Dispatchcomponent. We can also set a pattern on this component and, in this case, the pattern needs to be 0, 1, 1, 0 (untoggle Multiline Data). Output A returns the remaining points that we are looking for.

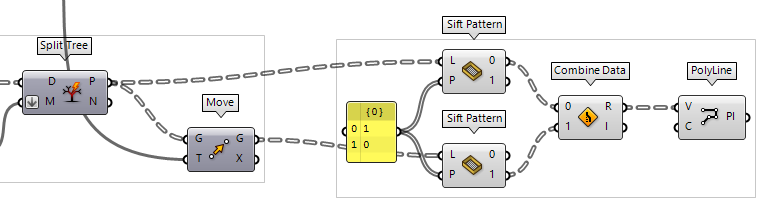
Sift Pattern and Combine Data

Unlike with Weave, where we reduced the number of points after combining them, we can also reduce the unnecessary points before combining. We do this with Sift Pattern. As pattern, we use 1 and 0 again and connect it to one Sift Pattern for the lower chords and one for the upper chords.

To combine them, we use Combine Dataand connect output 0 to input 0 and vice versa to get the zigzag. If you inspect the lists, you notice that Sift Pattern will not delete the unnecessary items but replaces them with Null Items. Combine Data will then fill the null items with items from the other list.