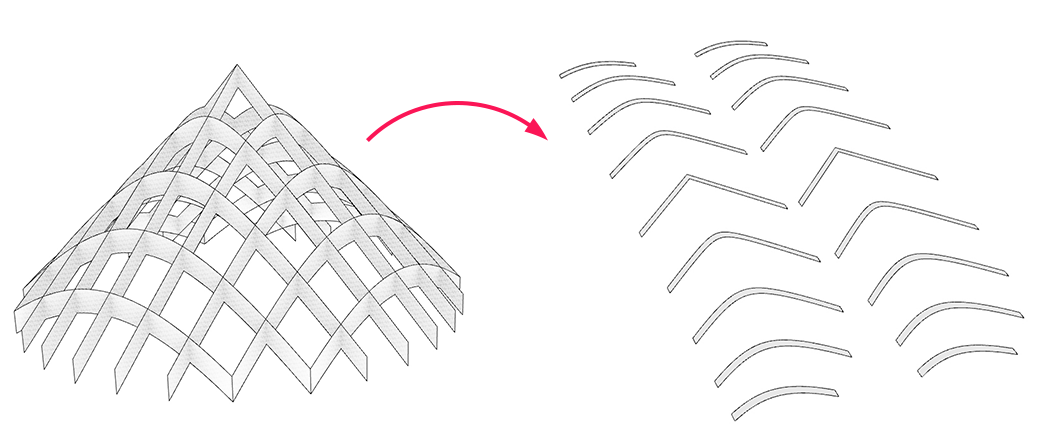
In this tutorial, we will generate slices from a 3d model and arrange them next to each other in one layer. This approach will work with any three-dimensional object; here we use a cone. The slices result from an intersection of the model with an array of planes. The generated section curves could be used for plotting or a CNC router.

Grasshopper

1

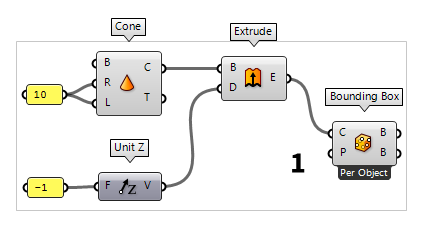
Define initial geometric object

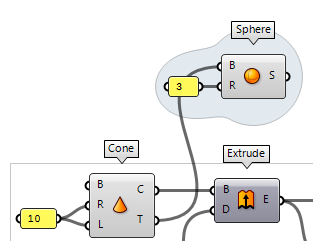
To start, we need a shape and in the following we will use a cone to illustrate the procedure. Thus, we place a Coneon the canvas and assign the value of 10 to the radius R and length L. By attaching an Extrudecomponent, we can turn the surface into a volumetric Brep. The direction D of the extrusion is given by a Unit Zvector and a material thickness of -1. A Bounding Boxwill then create a box around our cone. By default, the Bounding Boxcomponent will create a box for each object (as indicated by the label). If there are more objects, the component needs to be right-clicked and the option Union Box selected. This will wrap all objects in a single box. To change the orientation of the bounding box (and so the direction of the slices), we could provide a plane at input P.

Show Rhino Show Grasshopper

2

Generate section planes

To define section planes, we need an array of points that serve as origins for the planes. To find these points, we use Evaluate Boxand can then attach parameters to U and V. The parameters have to be normalized (between 0 and 1).

The component Rangewill generate N values within the domain D. By default, the domain is 0 To 1 and 10 ascending values are created. This is good enough for this exercise, but we need to use Cull Indexto remove the first (0) and last value (-1), which are the faces of the box. Then we connect the output of Range to the inputs U and V of Evaluate Box. This will give us the desired origin points at output Pt and we can connect a YZ Planeand an XZ Planeto get section planes in each direction.

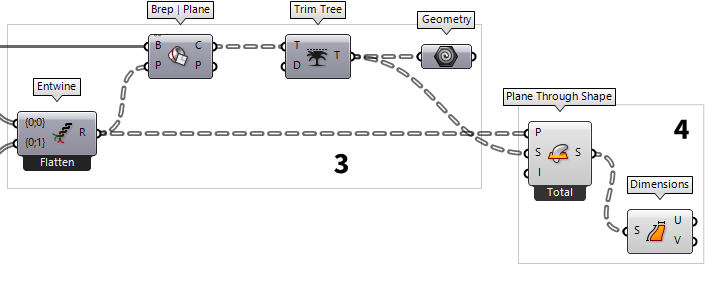
3

Compute section curves

While working with a Grasshopper algorithm, we have to ensure the data structures match the planed operation. In this case, we need a data treeand use Entwineto forward both lists of planes. Each list will become separate branches on a single tree. The ZUI can be used to remove the unneeded input grip.

Next, we place a Brep | Planecomponent on the canvas and connect our section planes and our solid (extruded cone) to it. At output C we find the curves that are created by solving the intersection event. But, each curve is in a separate branch and we need Trim Treeto remove the last separation level. Now we have two branches again; in each the curves for one direction. Optionally, we can bundle the curves in a Geometrycontainer. The first task, slicing the model, is completed and we will now arrange the section curves on one layer.

Show Rhino Show Grasshopper

4

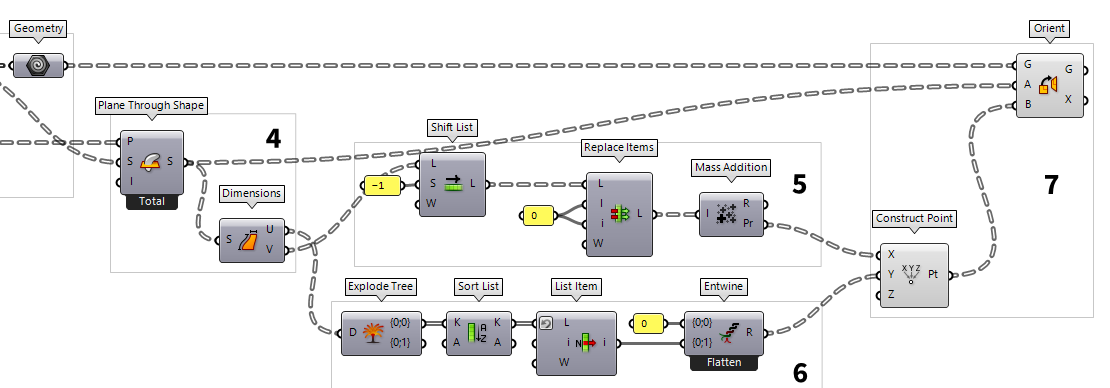
Get dimensions for arranging the curves in a plane

In the second half of this tutorial, we will arrange the slices in a single plane and next to each other, thus preparing them to be plotted on a sheet of paper. For this, we need coordinates for each slice that prevent overlapping of section curves. To get the dimensions, we use Plane Through Shape, which creates a wrapping rectangle in plane P for each curve S. The component Plane Through Shapeis similar to Bounding Box, but instead of a box with three dimensions, we get a planar, two-dimensional frame. The actual dimensions are calculated with the component Dimensions.

Show Rhino Show Grasshopper

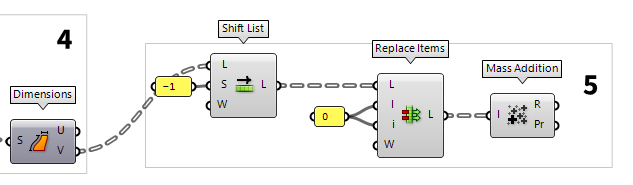
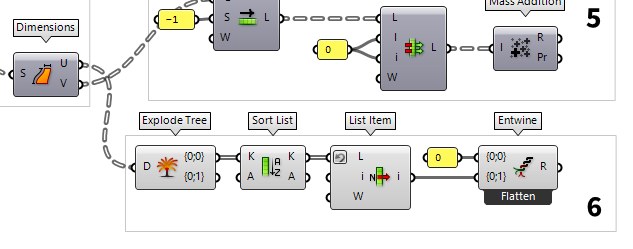
5

Find coordinates in x-direction

As stated, the coordinates for each slice on our base place depend on the dimensions of the section curves. Here, we would like to have two rows of section profiles, separated for each slicing direction. In x-direction we will place the curves from the same set and their distance is given by the height of each slice. The heights are obtained from output V of Dimensions.

The list of x-coordinates ought to start at 0, but currently starts with the first height. Therefore, we use Shift Listto offset the list by -1. Then we use Replace Itemsto replace the first item (index 0) in the list with 0.

The component Mass Additionsums all values in a list and also returns the intermediate results at output Pr. This is what we will use for the x-coordinates.

6

Find coordinates in y-direction

For the coordinates in y-direction, we will use a different approach, because here we will just have two rows, one for each set of curves. The distance of the rows is given by the largest width in the first set. The widths can be found at output U of Dimensionsand we use Explode Treeto separate the widths for each slicing direction. We are interested in the widths of the first branch {0,0}, which is also the first row of section curves.

To find the largest width, we use Sort Listto get an ascending order. Then, a List Itemcomponent will get the first value and thus we Reverse its input L to find the largest value. This will become the y-coordinate for the second row. The first row starts at 0 and we use Entwineto create two branches with one y-coordinate in each.

7

Arrange slices in a plane

After calculating the coordinates for each slice, we arrange them all in a single plane. To convert the coordinates to actual points, we will use Construct Pointand connect the inputs X and Y with the results from the previous two steps.

To place the section curves at their coordinates, we use Orient: Input G takes the geometric objects (our curves), input A the reference planes (result of Plane Through Shape) and input B the target planes (generated by connecting our coordinates).

Show Rhino Show Grasshopper

The result of this tutorial could now be plotted or fabricated with a CNC machine. It’s also possible to create slots at the slices' intersections to create a sliceform, which is explained in the tutorial Create a sliceform.

Test your skills

In the tutorial above, there was one geometric object to be sliced. Usually, we have more than one and now it’s your turn to tweak the algorithm so that it can handle several geometric objects. The section profiles on the base plane should contain all curves from one section. To keep it simple, let’s add a sphere to the tip of the cone.

Hint 1

Create the sphere

First, we create the sphere with Sphereand set a radius. Now, the sphere must become part of the algorithm.

Show Rhino Show Grasshopper

Hint 2

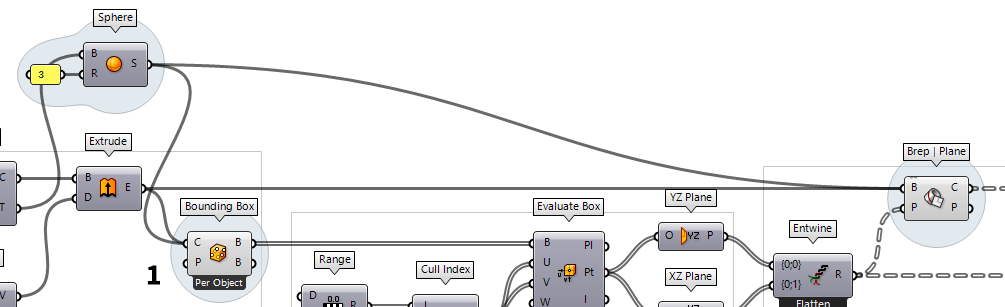
Connect the sphere

To include the sphere, we connect it to input C of Bounding Boxand to input B of the component Brep | Plane. But, this does not yet lead to the desired result and we need to change the handling of data in the algorithm.

Hint 3

Fix data structure

To change the data handling, we right-click the component Bounding Boxand select the option Union Box. This will create one box around all objects and not wrap each object with its own box.

Also, we have graft input P of Brep | Plane. Now, every section plane is in its own branch and every item at input B will be matched with every plane. This change will lead to an error: the component is displayed in red and states “Intersection failed”. But, this result is correct and could have been expected; the radius of the sphere is not large enough for it to have an intersection event with all the planes. We can ignore this error.

In the Rhino viewport, we can see that the arrangement on one layer is not yet working as expected. This is caused by the changed data structure; Plane Through Shapeneeds our attention.

Show Rhino Show Grasshopper

Hint 4

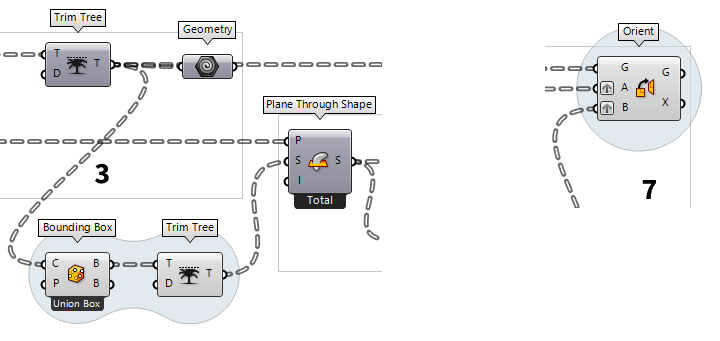
Capture the items in a single plane

The problem is that Plane Through Shapeis getting two items in each list, after solving the intersection with Brep | Planeand Trim Tree. Thus, Plane Through Shape creates a bounding rectangle for each item, but this is not what we want. Instead, we need a bounding rectangle both around items.

The Plane Through Shape component has no option for this and we use another Bounding Boxwith option Union Box selected. This way, we get flat boxes with no height. We have to reduce them by a branch level with Trim Treeand can now connect them to Plane Through Shapeto find the rectangle around all intersection curves in a slice. Instead of connecting the results from Bounding Box to Plane Through Shape, which is kind of an unnecessary repetition, we could have also extracted the right face from the box. But, more component would be needed.

As we can see, we still need to adjust Orientto handle the new data structure, which is done by grafing inputs A and B. Done.

Show Rhino Show Grasshopper