When working with curves in Grasshopper, it’s sometimes useful to remove duplicate curves. The more curves are processed in an algorithm, the longer does the computation take for each step. Also, duplicate curves might lead to mistakes in quantifycations and other calculations.

Kangaroo2 has a utility component removeDuplicateLinesthat will solve the said for lines and so does Karamba with Remove Duplicate Lines (Karamba3D). But, both components only allow lines to be processed. There might be a plugin that will solve this case for curves, but in this how-to guide we introduce two methods that work with vanilla Grasshopper. And yes, both methods will also work with lines.

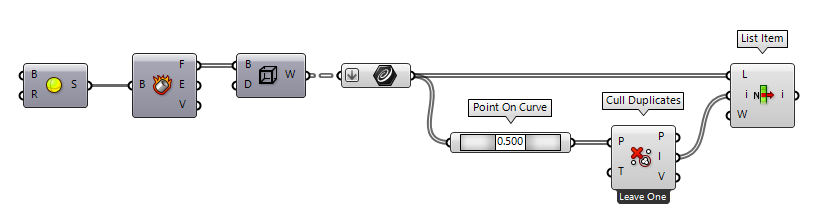
Remove duplicate curves (simple comparison)

Before we can remove anything, we have to identify the properties that duplicate curves share and which can be used to identify the duplicates. Often, it’s sufficient to check for identical midpoints. For example in those cases, when the duplicate curves were created by the edges of two adjacent surfaces.

The first step is to bundle all curves in a list and to flatten them if needed. Then we use Point On Curveto find the midpoints. We use the midpoints, because the endpoints might be flipped. The component Cull Duplicatescan be used to remove duplicate midpoints and thus, the corresponding curves can be identified. To get the indices we need from output I, we have to right-click the component and select Leave One. We can then attach a List Itemcomponent to get all unique curves.

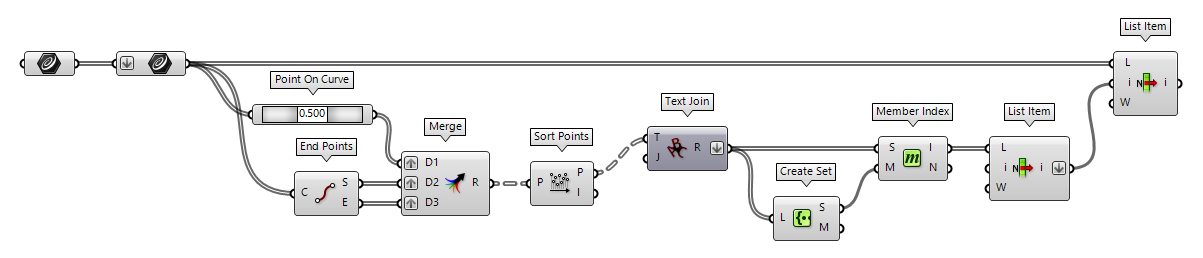
Remove duplicate curves (advanced comparison)

There can be cases in which deviant curves meet at their midpoints, for example in an X. With the previous method, those curves would be falsely identified as duplicates. If we suspect that this case might occur, we have to think of a more advanced method for comparison; one that takes various criteria into account. Then, if all criteria match, we can assume that the curves are congruent.

To proceed with this idea, we will concatenate the curves' attributes into a string, which we use a simplified hash value. Then we compare these hashes to identify duplicate curves. In this example, we will use the endpoints as additional attributes.

After bundling all curves, we will use Point On Curveand also End Points. Then, we Mergeall points and graft the inputs to get a list of points for each curve. We have to use Sort Pointsto equalize the drawing direction and Text Joinwill transform the points into a hash value.

Next, we flatten the hashes and use Create Setand Member Indexto create branches for curves with the same hash value. Each branch contains the references (indices) for the respective curves. Because we only need one curve each, we will use List Itemto get the first reference index from each list. Then, we flatten this list and connect it to another List Item, together with the initial curve bundle. We remain with the desired curves.