In general, it’s advised to generate meshes as late as possible in the algorithm because when we convert surfaces to meshes we lose topographic information. If possible, trim the surfacefirst and then convert the remaining surface into a mesh. Yet, this is not always possible, so this how-to guide illustrates different possibilities to trim a mesh depending on the trimming object and how to cap holes that were creating thereby.

Trim a mesh with another one

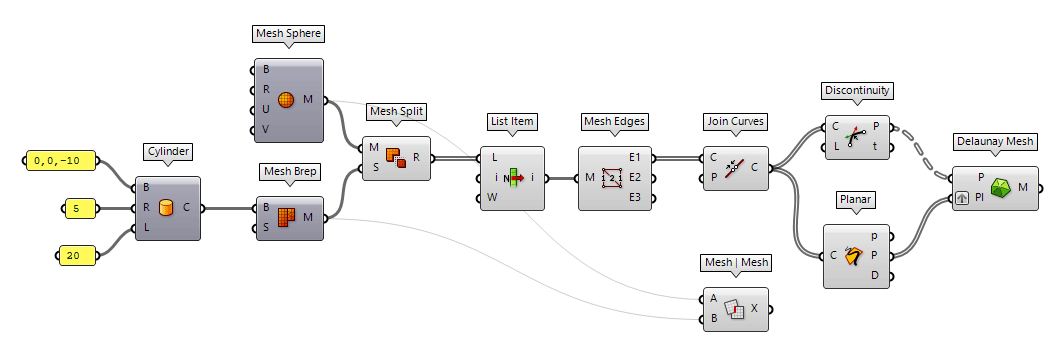
For this method, we look at random meshes and then trim one with the other. In the following, we have a sphere that is interpenetrated with a cylinder and the part of the sphere that is inside the cylinder will be cropped. Then, the created cutout is closed with a planar cap.

The component Mesh Spheredirectly generates the said sphere. For the cylinder, we use Cylinderto create the surface and set matching parameters. Next we use Mesh Brepto convert the cylinder into a mesh.

The component Mesh Splitwill split the sphere along the intersection curve with the cylinder. After the split, we get the remaining surface via List Item. In this case the preset value 0 of the index i is what we are looking for. Otherwise, we have to change the index or set up some components to calculate the index of the desired surface (it’s often the one with the largest area). We have now performed the trimming operation.

To close the remaining openings with another mesh, we first have to get the edges of the holes with Mesh Edgesand then we find them at output grip E1. Join Curveswill merge these edges to a polyline on each opening (this curves equal the intersection curves). Next, Discontinuitywill generate points at the vertices of the polylines and we use Planarto get the plane at each opening. Both are then combined to generate a Delaunay Meshthat caps the holes Using the Delaunay algorithm on the edge vertices will create a mesh in which some triangular faces span across the entire length of the opening. This generation is not adequate for FEM calculations. See the end of this page for an alternative solution.. In this example we have to graft the planes to match the data structure of the points.

As an alternative, we can also use the component Mesh | Meshto generate the intersection curves. This results in fewer components on the canvas but is slightly slower in computation, because the intense solving of intersections is done twice.

Trim a mesh with a plane

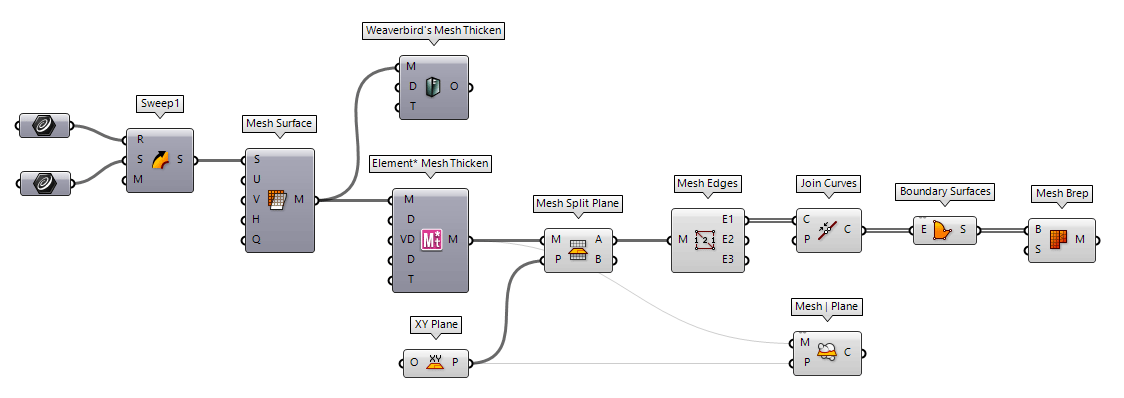
Another possibility to split a mesh is with a plane. Let’s assume is any mesh with an assigned thickness. This can be quickly done with the Grasshopper plugins Weaverbird or Element* and is a common scenario for 3D printing.

Now, we use Mesh Split Planeto split the mesh. We find the desired half of the mesh in one of the outputs. Just like above, we use Mesh Edgesand Join Curvesto obtain the intersection curves. And again, there is a computationally more expensive shortcut given by the component Mesh | Plane.

Unlike before, the intersection curve in this example has inflection points and the opening is concave. Thus, the Delaunay algorithm will not generate the desired mesh. We have to take a little detour by generating a Boundary Surfaceswithin each intersection curve and then convert them to a mesh with Mesh Brep.

Particularities of non-planar openings

In the examples above, the intersection curves were planar, which is not always true. For example, if two cylinders intersect, we get a twisted intersection curve. In case of meshed cylinders, this intersection curve is a polyline and there is no distinct method to cap the opening. We then have to think of an appropriate way that suits our design. In Grasshopper, Fragment Patchcan be used to create a Brep that technically covers a non-planar polyline, but the result might not be aesthetically pleasing.

For these twisted intersection curves, it’s easier to keep the solids as surfaces and solve there intersection. We can then use Patchto cover the twisted intersection curve in a more aesthetically pleasing way and this surface can be converted into a mesh.

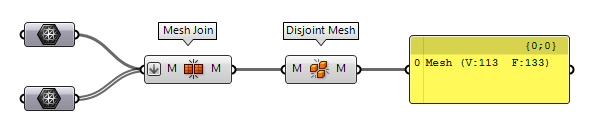
To check, whether the generated caps close the openings and everything forms is a tight union, we can combine the individual meshes with Mesh Join(don’t forget to flatten). We can then use Disjoint Meshand if the meshes shared a common typography, there still should be only one mesh. If there are more meshes as output than as input, the mesh edges of neighboring meshes were not aligned or the vertices were not lying on top of each other.

Particularities of other regular openings

The methods described above will not always be satisfying in some corner cases. For example if we need a mesh suitable for FEM calculations or have an intersection polyline that doesn’t deflect at every vertex. To solve these issues, we have to make sure that every vertex is part of the mesh or that additional faces are creating within the region of the opening.

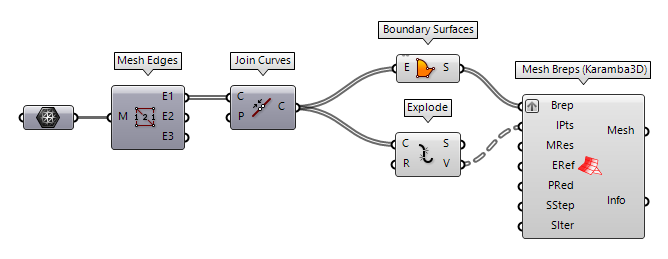
To solve the above, we can use Mesh Edgesand Join Curvesto generate the boundary curve, just like before. Besides creating Boundary Surfaces, we also use Explodeto deconstruct the intersection curve(s). This way, we get vertices separated for each curve. Karamba3D offers a special component Mesh Breps (Karamba3D)that generates meshes which include the provided points as mesh vertices.