In this how-to guide, we see how a polyline can be tweaked by adjusting specific points. If you need to rebuild or smooth a polyline based on a general characteristic, take a look the how-to Lines and polylines.

Find a specific vertex in a polyline

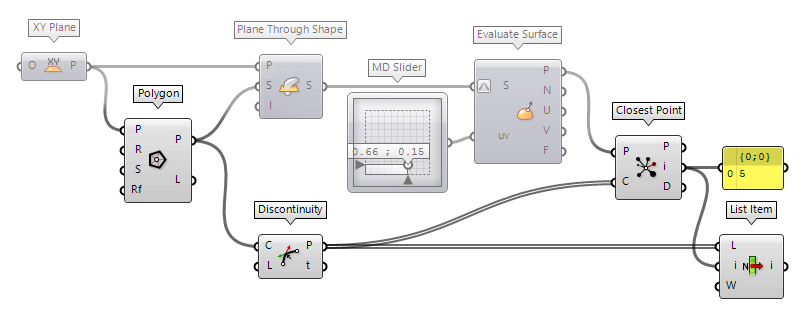
We can use different methods to find specific vertices in a polyline. In this example, we use a location based search, in which we have an existing point and find the vertex closest to it: After deconstructing the polyline, we find the Closest Pointfrom the vertices at C in relation to a given point at P. Output i emits the index of the desired vertex and we can use List Itemto grab it from the list of vertices.

Remove vertices from a polyline

To remove a vertex from a polyline, we can deconstruct it with either Discontinuityor Explodeand then use Cull Indexto remove a point at the specified index. Afterward, we use the remaining list to create a new PolyLine.

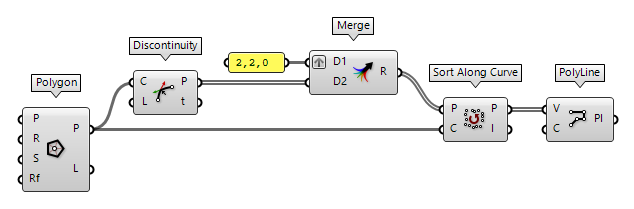
Add vertices to a polyline

To add a vertex to a polyline, we deconstruct it first and create a list with the new and existing vertices. Then, Sort Along Curvewill sort our list of points along the old polyline. This list is then used to create a modified PolyLinethat includes the new vertices.

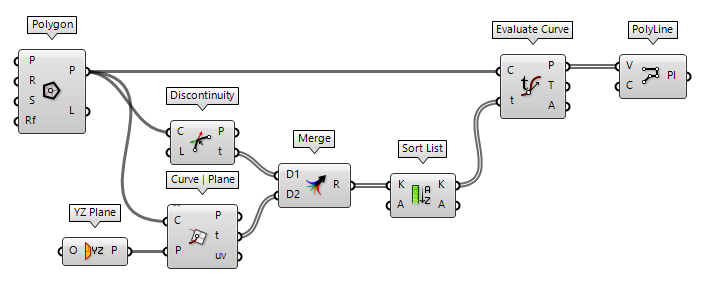
Another possibility, to add new vertices, is using the curve parameters of the existing polyline. Note that this approach is only possible, when the new vertices are on the existing polyline. Discontinuityreturns the existing curve parameters and we merge them in a list with new ones, which are, for example, obtained from an intersection event. This list is then sorted with Sort Listand we compute the points by connecting the curve parameters and the initial polyline to an Evaluate Curvecomponent. We create the new polyline with PolyLine.

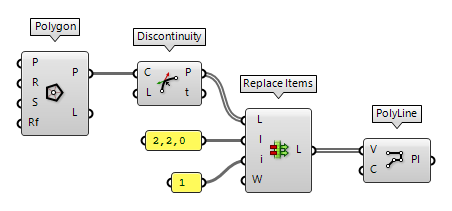
Replace vertices in a polyline

To replace a vertex, we deconstruct the polyline and use Replace Itemson the list of vertices. After modifying the desired point(s), we create a new PolyLine.

For advanced, yet specific, modifications, we can also make use of the full set of methods that are described in the how-to Filter lists.