This how-to guide provides the basic operations for lines and polylines. A line is, simply put, the straight connection between two points. Poly, from the Greek πολύς, means many or much and thus, a polyline is a construct that consists of several line segments. A polyline, or polygonal chain, is specified by a sequence of points; its vertices. The segments of a polyline can be converted to individual lines.
The edges of polygons, polyhedrons, and meshes are lines. The other way around, lines can be used to define these geometric shapes. A line is linear and its properties, except for the curve parameter, remain constant at every point. Lines are used in mathematical simulations, such as the Finite Element Method (FEM), Dynamic Relaxation, or particle-spring systems. If we wish to pursue such computations, we need to convert all curves to lines. Though a curve may be straight and resemble a line, it is another data type, and might therefore not be allowed. If a curve has changing properties along its course, it can be broken down into multiple lines with linearized properties.
Lines
Create lines
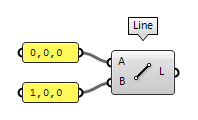
The simplest way to create a line is using the component Line Line (Ln)
Line (Ln)Inputs Start Point (A) Line start point End Point (B) Line end point Outputs Line (L) Line segment
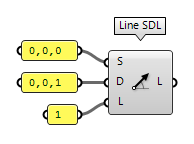
An alternative is to use Line SDL Line SDL (Line)
Line SDL (Line)Inputs Start (S) Line start point Direction (D) Line tangent (direction) Length (L) Line length Outputs Line (L) Line segment
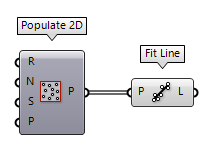
A line can also be created as a line of best fit for a collection of points, using
the component Fit Line Fit Line (FLine)
Fit Line (FLine)Inputs Points (P) Points to fit Outputs Line (L) Line segment
Convert curves to lines
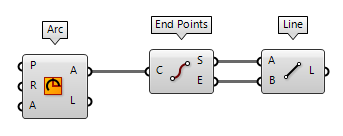
If we have a curve that we need to convert to a line, we can extract the End Points End Points (End)
End Points (End)Inputs Curve (C) Curve to evaluate Outputs Start (S) Curve start point End (E) Curve end point  Line (Ln)
Line (Ln)Inputs Start Point (A) Line start point End Point (B) Line end point Outputs Line (L) Line segment
Convert polylines to lines
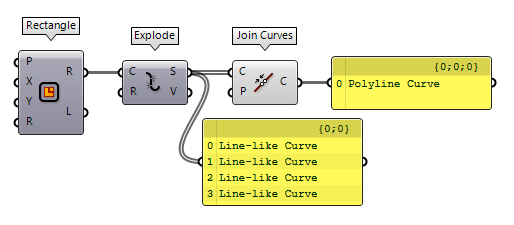
We can use Explode Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments
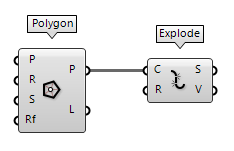
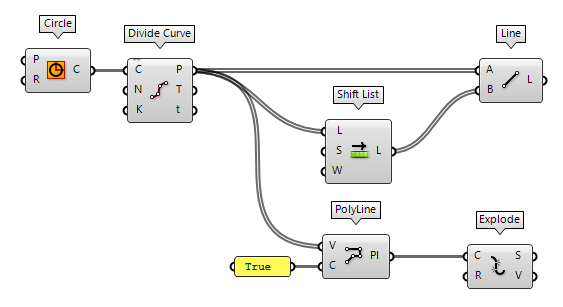
Convert closed curve to lines
To convert a closed curve, like a circle, to lines, we first have to create a
set of points on this curve and then we can use Shift List Shift List (Shift)
Shift List (Shift)Inputs List (L) List to shift Shift (S) Shift offset Wrap (W) Wrap values Outputs List (L) Shifted list  Line (Ln)
Line (Ln)Inputs Start Point (A) Line start point End Point (B) Line end point Outputs Line (L) Line segment
An alternative is using the points as vertices for a PolyLine PolyLine (PLine)
PolyLine (PLine)Inputs Vertices (V) Polyline vertex points Closed (C) Close polyline Outputs Polyline (Pl) Resulting polyline  Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments True to get a closed polyline.
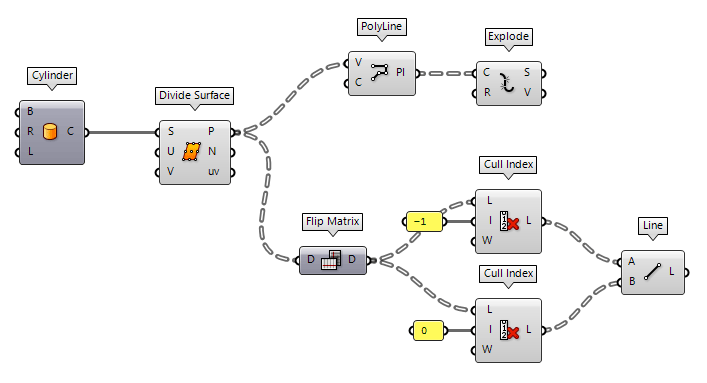
Convert grid points to lines
If we have a grid, or any ordered list of points, there are two methods to
create lines between the points. The first one is to create a PolyLine PolyLine (PLine)
PolyLine (PLine)Inputs Vertices (V) Polyline vertex points Closed (C) Close polyline Outputs Polyline (Pl) Resulting polyline  Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments
The second method uses the Line Line (Ln)
Line (Ln)Inputs Start Point (A) Line start point End Point (B) Line end point Outputs Line (L) Line segment  Cull Index (Cull i)
Cull Index (Cull i)Inputs List (L) List to cull Indices (I) Culling indices Wrap (W) Wrap indices to list range Outputs List (L) Culled list -1 to
remove the last item and Cull Index Cull Index (Cull i)
Cull Index (Cull i)Inputs List (L) List to cull Indices (I) Culling indices Wrap (W) Wrap indices to list range Outputs List (L) Culled list 0 to
remove the first item.
Polylines
Construct polylines
The component PolyLine PolyLine (PLine)
PolyLine (PLine)Inputs Vertices (V) Polyline vertex points Closed (C) Close polyline Outputs Polyline (Pl) Resulting polyline
If we have a collection of lines, we can use Join Curves Join Curves (Join)
Join Curves (Join)Inputs Curves (C) Curves to join Preserve (P) Preserve direction of input curves Outputs Curves (C) Joined curves and individual curves that could not be joined.
Also, every polygonal shape will automatically be converted to a polyline at a component’s input, which is requiring a curve.
Deconstruct polylines
To deconstruct a polyline, there are two components that can be used. Explode Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments  Discontinuity (Disc)
Discontinuity (Disc)Inputs Curve (C) Curve to analyze Level (L) Level of discontinuity to test for (1=C1, 2=C2, 3=Cinfinite) Outputs Points (P) Points at discontinuities Parameters (t) Curve parameters at discontinuities
Convert curves to polylines
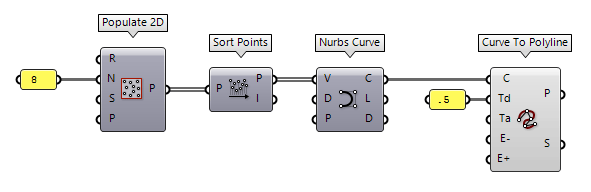
To convert a curve to a polyline, we can use Curve To Polyline Curve To Polyline (ToPoly)
Curve To Polyline (ToPoly)Inputs Curve (C) Curve to simplify Tolerance (distance) (Td) Deviation tolerance Tolerance (angle) (Ta) Angle tolerance in radians MinEdge (E-) Optional minimum allowed segment length MaxEdge (E+) Optional maximum allowed segment length Outputs Polyline (P) Converted curve Segments (S) Number of polyline segments
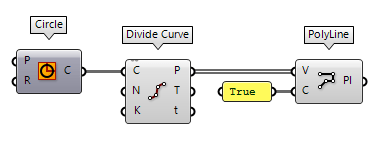
We can also divide a curve into segments of equal length with Divide Curve Divide Curve (Divide)
Divide Curve (Divide)Inputs Curve (C) Curve to divide Count (N) Number of segments Kinks (K) Split segments at kinks Outputs Points (P) Division points Tangents (T) Tangent vectors at division points Parameters (t) Parameter values at division points  PolyLine (PLine)
PolyLine (PLine)Inputs Vertices (V) Polyline vertex points Closed (C) Close polyline Outputs Polyline (Pl) Resulting polyline  Curve To Polyline (ToPoly)
Curve To Polyline (ToPoly)Inputs Curve (C) Curve to simplify Tolerance (distance) (Td) Deviation tolerance Tolerance (angle) (Ta) Angle tolerance in radians MinEdge (E-) Optional minimum allowed segment length MaxEdge (E+) Optional maximum allowed segment length Outputs Polyline (P) Converted curve Segments (S) Number of polyline segments
Rebuild polylines
In this section, we look at two approaches to rebuild or simplify a polyline based on its general characteristic. The first one is to remove some points while maintaining most of the polyline’s characteristics, the second approach is to create some kind of fitting polyline, thus reducing some of the peaks. If you would like to add or remove specific vertices or tweak a polyline at a certain point, you find the answers in the how-to Modify polylines.
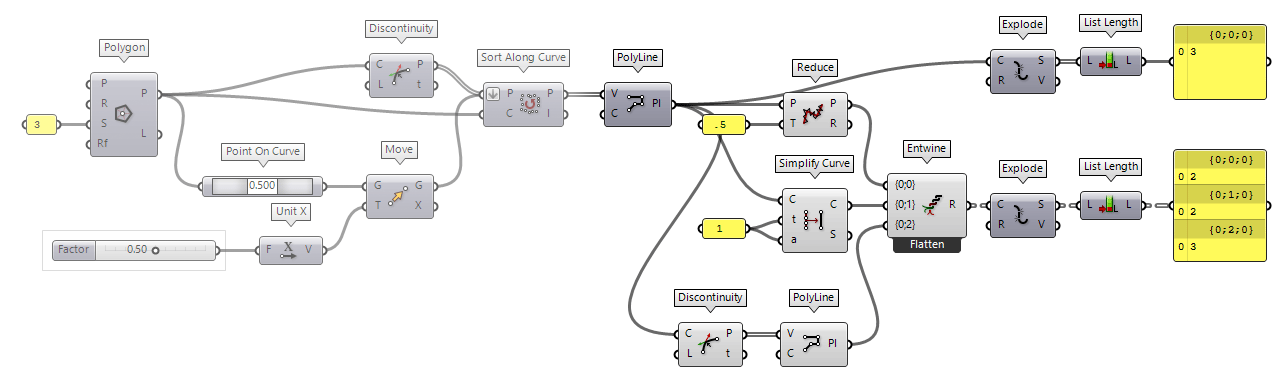
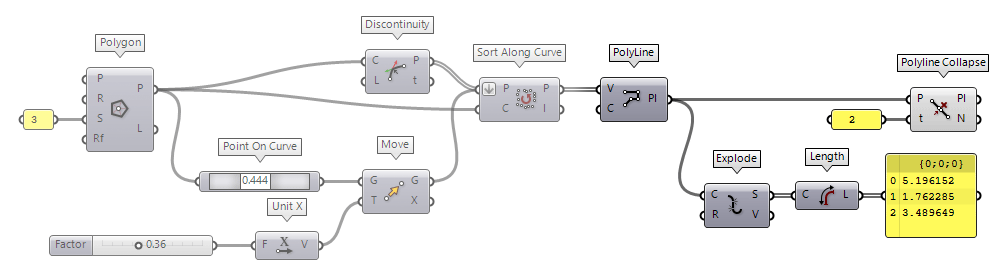
First, we take a look at a discreet modification of the polyline: If there are segments that have the same direction vector as the previous one, thus there is no kink at a vertex, we can remove this vertex without changing the characteristic of the polyline. To illustrate this, we use a polyline with two legs, but one leg has a point P in the middle, which can be set to deviate from its initial position to P' (see figure). Thus, the initial polyline consists of three segments; but visually, only two are recognizable.
With no kink, we have three options: The combination of Discontinuity Discontinuity (Disc)
Discontinuity (Disc)Inputs Curve (C) Curve to analyze Level (L) Level of discontinuity to test for (1=C1, 2=C2, 3=Cinfinite) Outputs Points (P) Points at discontinuities Parameters (t) Curve parameters at discontinuities  PolyLine (PLine)
PolyLine (PLine)Inputs Vertices (V) Polyline vertex points Closed (C) Close polyline Outputs Polyline (Pl) Resulting polyline  Reduce (RedPLine)
Reduce (RedPLine)Inputs Polyline (P) Polyline to reduce Tolerance (T) Tolerance (allowed deviation between original and reduction) Outputs Polyline (P) Reduced polyline Reduction (R) Number of vertices removed during reduction  Simplify Curve (Simplify)
Simplify Curve (Simplify)Inputs Curve (C) Curve to simplify Tolerance (t) Optional deviation tolerance (if omitted, the current document tolerance is used) Angle Tolerance (a) Optional angle tolerance (if omitted, the current document tolerance is used) Outputs Curve (C) Simplified curve Simplified (S) True if curve was modified in any way
Now, we move the point P by 0.5 to position P'. Also, we assign 0.5 as
tolerance T to Reduce Reduce (RedPLine)
Reduce (RedPLine)Inputs Polyline (P) Polyline to reduce Tolerance (T) Tolerance (allowed deviation between original and reduction) Outputs Polyline (P) Reduced polyline Reduction (R) Number of vertices removed during reduction 1 as tolerance t and as angle
a to Simplify Curve Simplify Curve (Simplify)
Simplify Curve (Simplify)Inputs Curve (C) Curve to simplify Tolerance (t) Optional deviation tolerance (if omitted, the current document tolerance is used) Angle Tolerance (a) Optional angle tolerance (if omitted, the current document tolerance is used) Outputs Curve (C) Simplified curve Simplified (S) True if curve was modified in any way
How do both components differ? Simplify Curve will handle all kinds of curves and we can set a deviation angle. Reduce will, if the polyline has a high amplitude and short frequency, reduce vertices and so the oscillation, while keeping the peak values. The component calls it the reduction of the least significant points and this could be useful for a dataset of measurements.
Another component to reduce the number of segments is Polyline Collapse Polyline Collapse (PCol)
Polyline Collapse (PCol)Inputs Polyline (P) Polyline curve Tolerance (t) Segment length tolerance Outputs Polyline (Pl) Resulting polyline Count (N) Number of segments that were collapsed 2. The component will now remove segments that are shorter
than the tolerance and create a new vertex V' at the midpoint of the removed
segment. The length and direction of the adjacent segments will change
accordingly.
This kind of operation can be useful, when lots of short lines are imported from
another source, for example an area map. We can use Join Curves Join Curves (Join)
Join Curves (Join)Inputs Curves (C) Curves to join Preserve (P) Preserve direction of input curves Outputs Curves (C) Joined curves and individual curves that could not be joined.
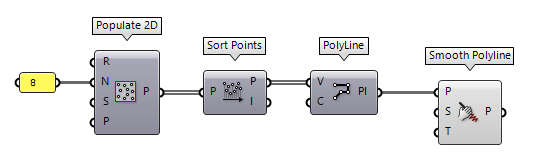
To address the second approach, creating some kind of fitting curve with the
initial vertices, we can use the component Smooth Polyline Smooth Polyline (SmoothPLine)
Smooth Polyline (SmoothPLine)Inputs Polyline (P) Polyline to smooth Strength (S) Smoothing strength (0 = none, 1 = maximum) Times (T) Number of times to apply the smoothing operation Outputs Polyline (P) Smoothed polyline