This how-to guide will focus on how to divide a curve with pattern-based rules. These rules are given by the designer within the algorithm and do not necessarily rely on any event. To see how curves can be split at intersection events, see Split curves.
The components that are introduced below output the coordinates for the division
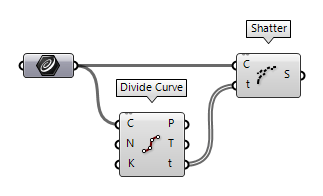
points and the curve parameters t, which can be used with Shatter Shatter (Shatter)
Shatter (Shatter)Inputs Curve (C) Curve to trim Parameters (t) Parameters to split at Outputs Segments (S) Shattered remains
Divide a curve in n segments (Divide Curve)
The component Divide Curve Divide Curve (Divide)
Divide Curve (Divide)Inputs Curve (C) Curve to divide Count (N) Number of segments Kinks (K) Split segments at kinks Outputs Points (P) Division points Tangents (T) Tangent vectors at division points Parameters (t) Parameter values at division points True, the output will also
include the parameters at the kinks.  Discontinuity (Disc)
Discontinuity (Disc)Inputs Curve (C) Curve to analyze Level (L) Level of discontinuity to test for (1=C1, 2=C2, 3=Cinfinite) Outputs Points (P) Points at discontinuities Parameters (t) Curve parameters at discontinuities  Discontinuity (Disc)
Discontinuity (Disc)Inputs Curve (C) Curve to analyze Level (L) Level of discontinuity to test for (1=C1, 2=C2, 3=Cinfinite) Outputs Points (P) Points at discontinuities Parameters (t) Curve parameters at discontinuities  Shatter (Shatter)
Shatter (Shatter)Inputs Curve (C) Curve to trim Parameters (t) Parameters to split at Outputs Segments (S) Shattered remains
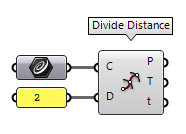
Divide a curve by distance (Divide Distance)
The component Divide Distance Divide Distance (DivDist)
Divide Distance (DivDist)Inputs Curve (C) Curve to divide Distance (D) Distance between points Outputs Points (P) Division points Tangents (T) Tangent vectors at division points Parameters (t) Parameter values at division points
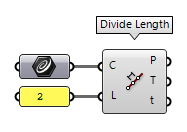
Divide a curve by length (Divide Length)
The component Divide Length Divide Length (DivLength)
Divide Length (DivLength)Inputs Curve (C) Curve to divide Length (L) Length of segments Outputs Points (P) Division points Tangents (T) Tangent vectors at division points Parameters (t) Parameter values at division points
Divide Length divides the curve into n segments with the same length (except
for the last one). To divide a curve into segments with varying length, we can
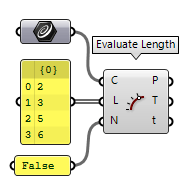
use Evaluate Length Evaluate Length (Eval)
Evaluate Length (Eval)Inputs Curve (C) Curve to evaluate Length (L) Length factor for curve evaluation Normalized (N) If True, the Length factor is normalized (0.0 ~ 1.0) Outputs Point (P) Point at the specified length Tangent (T) Tangent vector at the specified length Parameter (t) Curve parameter at the specified length False to prevent
normalization and provide a list of lengths at input L. Note that the
lengths that we provide to not relate to the step size (length of the segments)
but to the length parameter from the start of the curve.
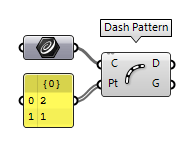
Divide curve into a dash patter (Dash Pattern)
The component Dash Pattern Dash Pattern (Dash)
Dash Pattern (Dash)Inputs Curve (C) Curve to dash Pattern (Pt) An collection of dash and gap lengths. Outputs Dashes (D) Dash segments Gaps (G) Gap segments  Divide Length (DivLength)
Divide Length (DivLength)Inputs Curve (C) Curve to divide Length (L) Length of segments Outputs Points (P) Division points Tangents (T) Tangent vectors at division points Parameters (t) Parameter values at division points  Shatter (Shatter)
Shatter (Shatter)Inputs Curve (C) Curve to trim Parameters (t) Parameters to split at Outputs Segments (S) Shattered remains  Cull Pattern (Cull)
Cull Pattern (Cull)Inputs List (L) List to cull Cull Pattern (P) Culling pattern Outputs List (L) Culled list
The dash pattern does not have to be a single number, but can also be a list of numbers. The pattern expresses the step size and is repeated until the curve is consumed (the pattern shown below does the same splitting as the pattern inputted to Evaluate Length in the second last figure).
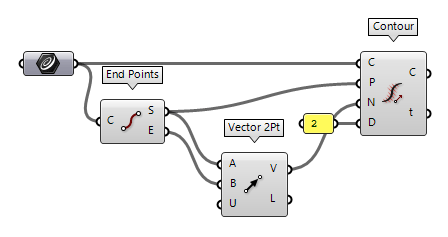
Divide a curve with contour lines (Contour)
The component Contour Contour (Contour)
Contour (Contour)Inputs Curve (C) Curve to contour Point (P) Contour start point Direction (N) Contour normal direction Distance (D) Distance between contours Outputs Contours (C) Resulting contour points (grouped by section) Parameters (t) Curve parameters for all contour points
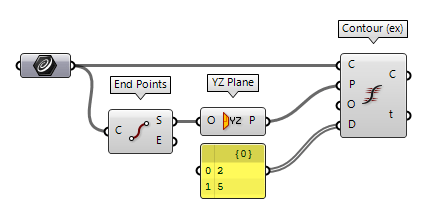
The component Contour (ex) Contour (ex) (Contour)
Contour (ex) (Contour)Inputs Curve (C) Curve to contour Plane (P) Base plane for contours Offsets (O) Contour offsets from base plane (if omitted, you must specify distances instead) Distances (D) Distances between contours (if omitted, you must specify offset instead) Outputs Contours (C) Resulting contour points (grouped by section) Parameters (t) Curve parameters for all contour points