Trimming curves implies that we split the curves and dump one of their remaining segments. Thus, we have to define the cutter and also, which side of the boundary contains the objects that will be disposed. The object can relate to the cutter in three ways:

1. The object is completely inside the trimming area.
2. The object has an intersection with the cutter.
3. The object is completely outside the trimming area.

outside

object with intersection

inside the trimming area

The first step of trimming is to split all curves that have an intersection with the cutting shape, which is explained in the how-to Split curves. Then, we should combine all curves (cut and uncut) in a single data tree, which can be achieved with Combine Data. Now, we eliminated the second possibility and all curves are either inside or outside our trimming area.

To check, whether a curve should be kept or disposed, we will retrieve its midpoint and then check if this point is inside or outside the trimming area. The midpoints are generated with Point On Curve. We could also use the component Curve Middle(new in Rhino 6.16). For the query, we need a list of Boolean values (True or False) which determine the state of each curve. How we get this list depends on the cutting objects:

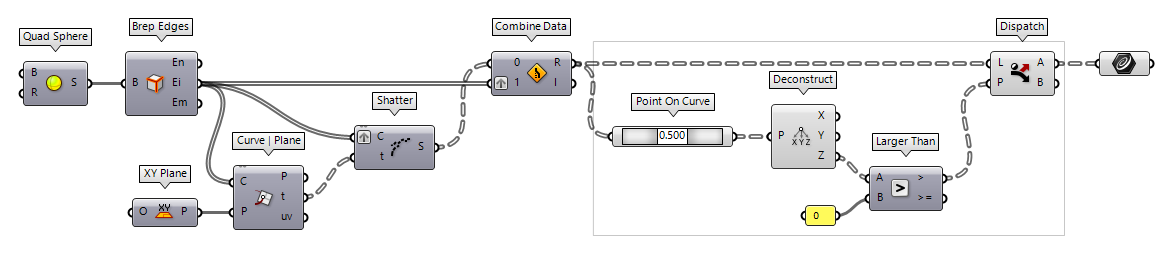
Trim curves with a plane

After splitting the curves with an XY Planeand bundling them in a data tree, we use Point On Curveto retrieve their midpoints. By attaching a Deconstructcomponent to the midpoints, we can get the Z-coordinate. We then use Larger Thanto determine if the z-coordinate of the curve is above (True) or below (False) the Z-coordinate of the plane (here 0). We can use Dispatchto sort the curves according to the list of Boolean values and, in this example, output A will contain all curves above our plane.

If we have an XZ Plane, a YZ Plane, or the origin of the plane is not at 0, we need to match this setup with the values we use for comparison on the components Deconstructand Larger Than.

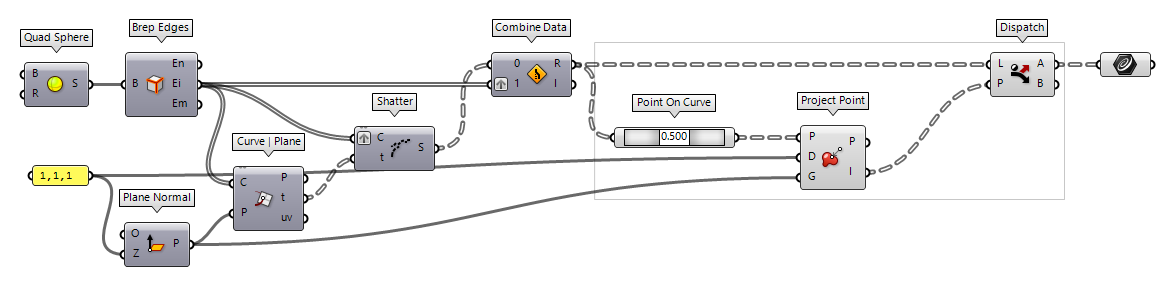
If we use a construction plane that is tilted in space, we can use Project Pointto project the midpoints onto the plane and set the projection direction D to the normal of the plane. Output I will now return 0 or -1 depending on whether a point hits the plane with the given direction. This output can be used with Dispatchto separate the curves.

Trim curves with a cutting curve

When we need to trim curves that are inside or outside a boundary curve, we can use a closed cutting curve (as in the schematic sketch at the beginning). Again we use Point On Curveto get the midpoints and then we check with Point In Curveif the curves' midpoints are inside the boundary curve. Output R provides this information (0 = outside, 1 = coincident, 2 = inside) and we use Sift Patternto sort accordingly (zoom in to add another output grip). Now output 0 contains all curves that are outside our cutting shape.

Trim curves with a cutting solid

In cases where all curves are arbitrarily orientated in the three-dimensional space, we can use a solid as boundary for the trim. To check if a midpoint is inside a solid (here a Domain Box), we use Point In Brep. A Dispatchcomponent will do the separation and we can then find all curves that are outside the solid at output B.