Kangaroo
Physics by Daniel Piker is a physics engine
for simulation and constraint solving. It can be used within Grasshopper to find
a physical equilibrium and to interactively explore different configurations of
an idea. Kangaroo 2 comes preinstalled with Rhino 6 and higher and is not
compatible with Kangaroo 0.099. Just like form-finding
Using Kangaroo typically follows a similar line of action: We have to set up our experimental playground in which the magic can happen. The most important takeaway is, that we basically rebuild our model with Kangaroo components. They are called goals and each goal brings a certain energy into the system. The Kangaroo solver then tries to find the state in which the sum of all energies acting in the system is as low as possible. Every geometry or behavior that we don’t remodel will not be part of our physical simulation. This may sound obvious, but it’s the most common reason why we don’t get what we anticipated.
Grasshopper
In this introductory example, we will create a four-point sail, which is an architectural membrane fixed to four points, two high and two low points. We will turn those four points into anchors, find a representation for the membrane and introduce tension to find the typical shape of a stretched fabric.
1
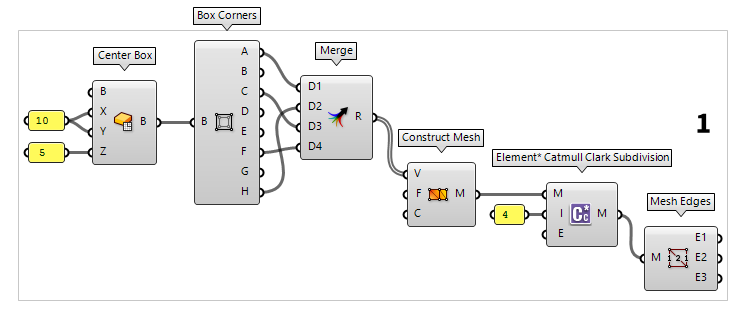
Create basic geometry
To generate the four points for our sail, we will create a Center Box Center Box (Box)
Center Box (Box)Inputs Base (B) Base plane X (X) Size of box in {x} direction. Y (Y) Size of box in {y} direction. Z (Z) Size of box in {z} direction. Outputs Box (B) Resulting box  Box Corners (Box Corners)
Box Corners (Box Corners)Inputs Box (B) Base box Outputs Corner A (A) Corner at {x=min, y=min, z=min} Corner B (B) Corner at {x=max, y=min, z=min} Corner C (C) Corner at {x=max, y=max, z=min} Corner D (D) Corner at {x=min, y=max, z=min} Corner E (E) Corner at {x=min, y=min, z=max} Corner F (F) Corner at {x=max, y=min, z=max} Corner G (G) Corner at {x=max, y=max, z=max} Corner H (H) Corner at {x=min, y=min, z=max}  Merge (Merge)
Merge (Merge)Inputs Data 1 (D1) Data stream 1 Data 2 (D2) Data stream 2 Outputs Result (R) Result of merge
We will then create a mesh between our four points with Construct Mesh Construct Mesh (ConMesh)
Construct Mesh (ConMesh)Inputs Vertices (V) Vertices of mesh object Faces (F) Faces of mesh object Colours (C) Optional vertex colours Outputs Mesh (M) Constructed mesh  Element* Catmull Clark Subdivision (CC)
Element* Catmull Clark Subdivision (CC)Inputs Mesh (M) Input a polygon Mesh Iterations (I) Input Integer specifying the Number of Subdivision Iterations Edge Condition (E) Input integer Value list to specify edge condition type (0 = Fixed | 1 = Smooth | 2 = Corners Fixed) Outputs Subdivided Mesh (M) Outputs the new subdivided polygon Mesh  Weaverbird's Catmull-Clark Subdivision (wbCatmullClark)
Weaverbird's Catmull-Clark Subdivision (wbCatmullClark)
Provided by Weaverbird 0.9.0.1.Inputs Mesh/Curves (M) The open or closed mesh, or closed curves list, to subdivide Level (L) The number of subdividing iterations for each face Smooth Naked Edges (S) Defines how to treat the naked edges
0: Fixed. Naked edges will not move or be modified.
1: Smooth. The naked edge will tend toward a spline.
2: Corner Fixed. Corners (2-sided vertices) will be fixed, while other naked vertices will tend toward a spline.Outputs Output Mesh/Curves (O) The mesh after the subdividing process  Weaverbird's Catmull-Clark Subdivision (wbCatmullClark)
Weaverbird's Catmull-Clark Subdivision (wbCatmullClark)
Provided by Weaverbird 0.9.0.1.Inputs Mesh/Curves (M) The open or closed mesh, or closed curves list, to subdivide Level (L) The number of subdividing iterations for each face Smooth Naked Edges (S) Defines how to treat the naked edges
0: Fixed. Naked edges will not move or be modified.
1: Smooth. The naked edge will tend toward a spline.
2: Corner Fixed. Corners (2-sided vertices) will be fixed, while other naked vertices will tend toward a spline.Outputs Output Mesh/Curves (O) The mesh after the subdividing process 4 iterations). The
component Mesh Edges Mesh Edges (MEdges)
Mesh Edges (MEdges)Inputs Mesh (M) Mesh for edge extraction Outputs Naked Edges (E1) Edges with valence 1 (a single adjacent face) Interior Edges (E2) Edges with valence 2 (two adjacent faces) Non-Manifold Edges (E3) Edges with valence 3 or higher
2
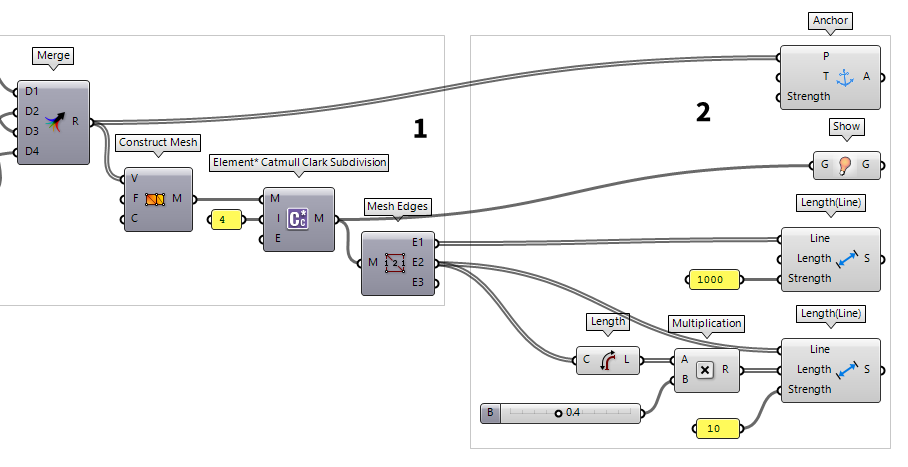
Reconstruct geometry as goals
With the completion of step 1, we have a geometrical description of all our
objects, and we will now construct a goal for each element that needs to be
included in our physical model. We start with the four points and connect them
to an Anchor Anchor (Anchor)
Anchor (Anchor)Inputs Point (P) Point to anchor Target (T) Location to pull the anchor to. If left empty, the initial location will be used. Strength (Strength) Strength Outputs A (A) Anchor out
Architectural membranes are not connected to the supports directly, but to an
edges cable that is used to stretch the membrane and carry the loads to the
supports. To simulate the edge cable, we attach the naked edges to a Length(Line) Length(Line) (Length(Line))
Length(Line) (Length(Line))Inputs Line (Line) Line Length (Length) Length - If none provided, starting length will be used Strength (Strength) Strength Outputs Spring (S) Spring out 1000. This
component’s goal is to assign all inputted Lines the provided Length. If
no length is provided, the original length is used.
For all interior edges we calculate their initial length with Length Length (Len)
Length (Len)Inputs Curve (C) Curve to measure Outputs Length (L) Curve length  Multiplication (A×B)
Multiplication (A×B)Inputs A (A) First item for multiplication B (B) Second item for multiplication Outputs Result (R) Result of multiplication  Number Slider
Number Slider Length(Line) (Length(Line))
Length(Line) (Length(Line))Inputs Line (Line) Line Length (Length) Length - If none provided, starting length will be used Strength (Strength) Strength Outputs Spring (S) Spring out 10.
What will happen during the calculation is that the solver tries to satisfy all
goals, but because they are opposed, it cannot. Thus, the stronger goals will
have a greater impact. In this case, the edge cables want to keep their length
and the interior edges try to shorter themselves. As the strength of the edge
cables is higher, their objective is also ranked higher, and they will deform
less than the interior edges. The fix points, by default, have a Strength of
10000 and therefore they deviate fewest of all.
For visualization purposes we also add a Show Show (Show)
Show (Show)Inputs G (G) Geometry Outputs G (G) Connect to GoalFunctions input
3
Solve physical interaction
Now, we have all pieces of the puzzle and we will let Kangaroo Physics solve
it by finding an equilibrium. All goals are connected to the input
GoalObjects of a Solver Solver (Solver)
Solver (Solver)Inputs GoalObjects (GoalObjects) GoalObjects Reset (Reset) Hard Reset (completely rebuild the particle list and indexing) Threshold (Threshold) Stop when average movement is less than this (default is 1e-15) Tolerance (Tolerance) Points closer than this distance will be combined into a single particle On (On) If true, Kangaroo will continue to iterate until reaching the given threshold value Outputs I (I) Iterations V (V) V O (O) GoalFunction Output tree  Button (Button)
Button (Button) Boolean Toggle (Toggle)
Boolean Toggle (Toggle)
When the toggle is switched to True the solver is iterating and the current number of iterations can be found at output I. The message underneath the component states the current status of the solver, whether it is paused, running or has converged. At output O, we find our form-found objects.
Test your skills
As mentioned in the side note, we actually applied tension to the membrane by giving it the goal to become smaller. In reality, we would move the support nodes outwards. Now it’s your turn to model this behavior within Kangaroo.
Move supports outward
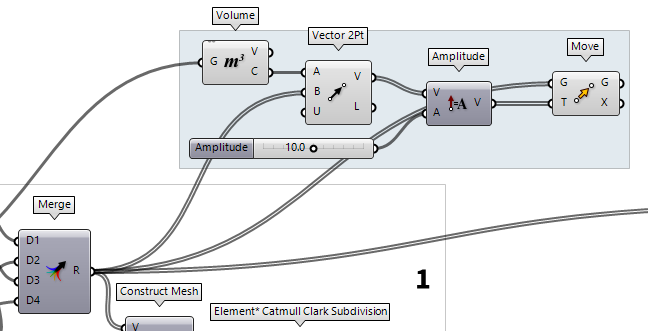
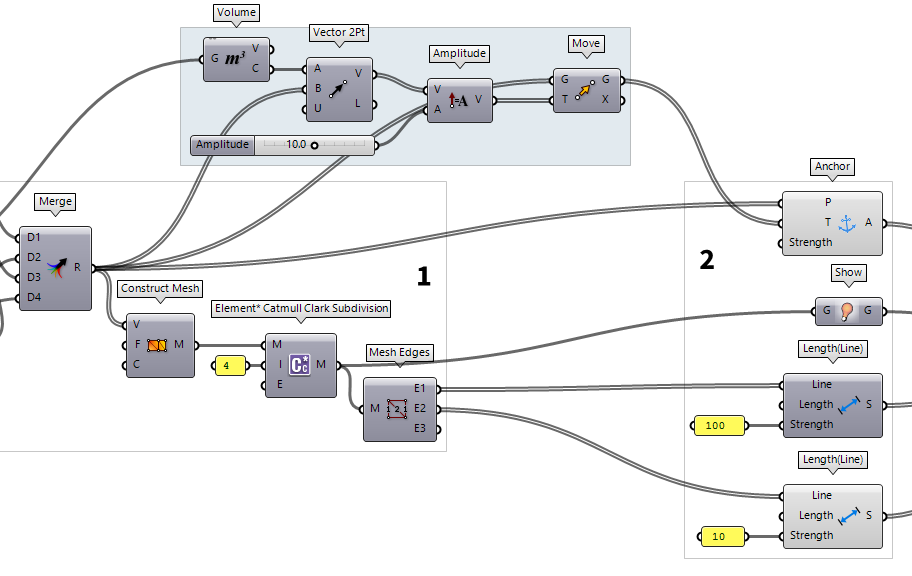
We start with moving the fixed
points outward. This can be done by calculating the center point of the box with
Volume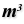 Volume (Volume)
Volume (Volume)Inputs Geometry (G) Closed brep or mesh for volume computation Outputs Volume (V) Volume of geometry Centroid (C) Volume centroid of geometry  Vector 2Pt (Vec2Pt)
Vector 2Pt (Vec2Pt)Inputs Point A (A) Base point Point B (B) Tip point Unitize (U) Unitize output Outputs Vector (V) Vector Length (L) Vector length
We use a Move Move (Move)
Move (Move)Inputs Geometry (G) Base geometry Motion (T) Translation vector Outputs Geometry (G) Translated geometry Transform (X) Transformation data  Amplitude (Amp)
Amplitude (Amp)Inputs Vector (V) Base vector Amplitude (A) Amplitude (length) value Outputs Vector (V) Resulting vector  Number Slider
Number Slider
Next, we have to implement this setup somehow as goals for Kangaroo.
Set new supports as target
The artificial shortening of our interior edges is no longer needed and can be removed.
If we connect our displaced points as new anchor points, there would be no
physical connection between them and the rest of our model. Thus, we add them as
target T to our existing Anchor Anchor (Anchor)
Anchor (Anchor)Inputs Point (P) Point to anchor Target (T) Location to pull the anchor to. If left empty, the initial location will be used. Strength (Strength) Strength Outputs A (A) Anchor out
After hitting the reset button, we get the new form-found membrane.