This how-to guide will recap various methods to split curves at intersection events and how to get the remaining segments. The how-to Divide curves is focusing on a segmentation with a regular or pattern-based logic. To select the curves behind or before the intersecting shape and how to remove them, see Trim curves.

For the general purpose splitting of curves, we can use the component Shatter. Input C takes the curves to split and input t is asking for the curve parameter to split at. The parameter t is therefore no point, but relates the distance from the curve’s start to the desired mark. Therefore, before we can do any splitting, we have to compute the necessary values for t.

In simple cases, there is no need to calculate the parameter to split at, because we can directly set it. For example, if we would like to split a line or regular curve in the middle, we can reparameterize the curve and set t to 0.5. Note that for complex curves, like Nurbs curves, the midpoint might not be at parameter 0.5.

Calculate curve parameters for splitting

As said, before we can do the actual splitting, we have to compute the parameters to split at. The ribbon tab Intersect contains components for different intersection events. Some components will directly output the sought-for curve parameters t, while others just emit the intersection point P and we have to retrieve the splitting parameter t with an extra step.

Find parameters to split at a component’s output (two distinct sets of curves)

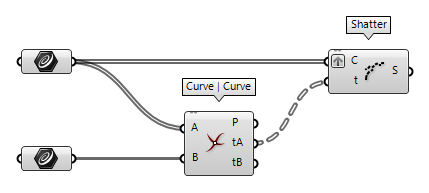
Given are two sets of curves: Set A contains vertical curves and set B consists of one horizontal curve. We can solve the intersection of the two sets with the component Curve | Curve. Beside the actual intersection points P, we also get the curve parameters for each set, tA for set A and tB for set B. Now, we connect the curves from set A and the curve parameters tA to a Shattercomponent. We also have to graft to adjust the data structureat input C.

B

A

A

A

A

A

This procedure will split the curves in Set A. If we wish to also split set B, we have to use another Shattercomponent in a corresponding way.

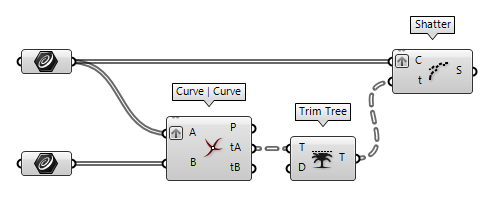
Next, let us assume that there is another horizontal curve in set B (the wire has now switched to two parallel lines). To ensure that every curve from one set is compared with each curve from the other set, we have to adjust the data structure and graft either of the two input grips of Curve | Curve. After solving the intersection, we have to reduce the data tree by one level, which is done with Trim Tree. Then we can use Shatterfor splitting the curves.

A similar procedure can be used with the components Line | Line, Curve | Line, Curve | Selfand a few others in the ribbon tab Intersect.

Find parameters to split at a component’s output (unsorted bundle of curves)

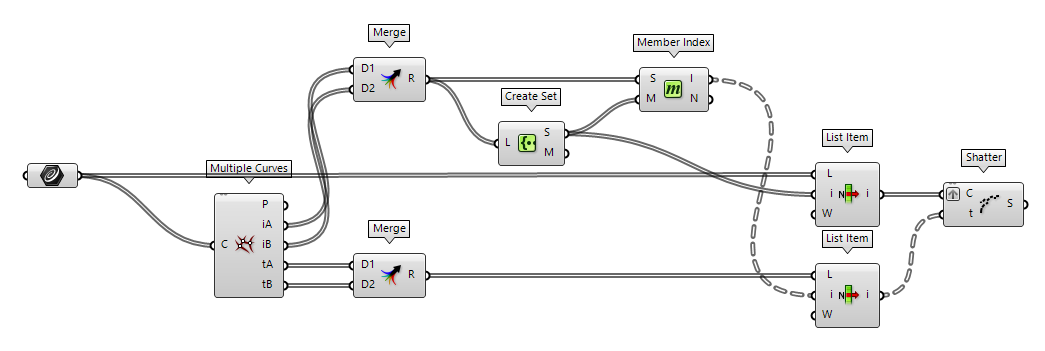
If all curves are bundled in a single list and there is no distinct set to solve the intersection event for, we can use Multiple Curvesto compare every curve with every other. Even though we get the curve parameters for each curve (tA and tB) there is no simple output that gives us the corresponding curves: The outputs iA and iB state the indices of the curves that each intersection events belongs to, but we have to manually sort the curves and group all intersections that each curve is subject to.

To proceed, we will first bundle our outputs with Merge, so that both lists correspond to each other. Then we use Create Setand Member Indexto create a data tree in which each branch holds a unique curve index. The number of index repetitions in each branch is given by the number of intersection events for each curve. See Filter lists for more information about this strategy. Then we can use List Itemto retrieve the curves that we want to split from output S of Create Set. We also need another List Itemto group the curve parameters for each curve. Finally, we use Shatterto do the splitting.

Compute parameters to split with intersection points

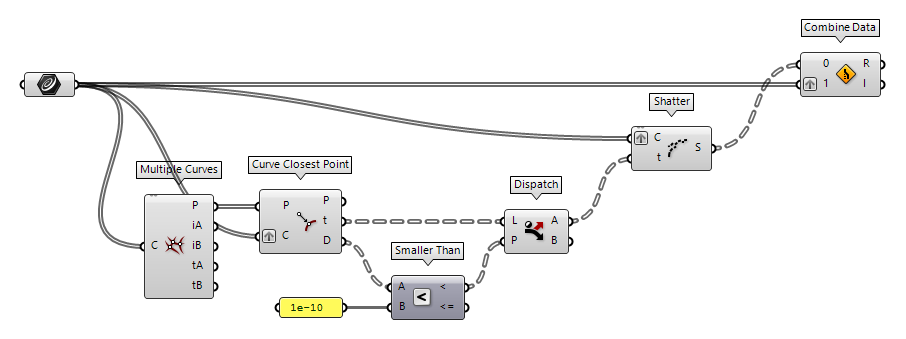
For this example, we take the unsorted bundle of curves from the previous chapter and again, we use Multiple Curvesto solve their intersection events. Unlike before, we are not using the curve parameters to proceed but instead the intersection points at output P. In order to use Shatter, we have to compute the curve parameters with a different method: Curve Closest Pointwill generate the closest point on a curve in relation to a given point.

After grafting input C of Curve Closest Point, we compute the distance of every intersection point to every curve. But we are only interested in the points that are actually on the curves. To get them, we use Smaller Thanand Dispatchto select the desired curve parameters t for points that have no distance D to the curve. Instead of 0 we use 1e-10 to account for software-related inaccuracies.

Shatterwill split our curves into segments. But, as mentioned before, curves that had no intersection event will not be part of the output. To create a data tree that contains all curves, we can use Combine Data. This is useful if we would like to continue with a trimming action.

A similar procedure can be used with the components Brep | Curve, Surface | Curve, Curve | Plane, Mesh | Curveand others in the ribbon tab Intersect, which do not emit a curve parameter t but intersection points.