In this tutorial, we will create a typical space frame roof and continue to get familiar with Grasshopper. You can read more about the structural idea of space frames on this page.

Planar space frames are typically created by combining different types of polyhedra. For the following exercise we choose the combination of two platonic solids: Half-octahedron and tetrahedron (see figure below). Alternatively, we can imagine the space frame as two parallel, mutually shifted square grids, which are separated from each other by the distance $h$ and whose nodes are connected by spatial diagonals.

Tetrahedron

Half-Oktahedron

$h$

$a$

In this tutorial, we set the base length $a = 1$ and thus the distance is $h = 1 / 2 \cdot \sqrt 2 = 0,707$.

Grasshopper

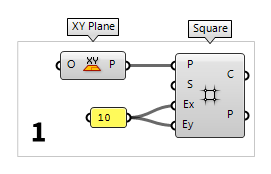
1

Generate top grid

First thing to do is to create a grid. We do this by placing the component Squareon the canvas. We could use input S to define a cell size, but this component uses already the desired value 1 as its default value. We can see the preset value by hovering the input grip with the mouse cursor.

The inputs Ex and Ey determine the number of cells that are generated in the respective direction of the square grid. If we type "10 into the canvas search, we get a Panelwith the value 10. After connecting this panel to the inputs Ex and Ey, a grid with 10 × 10 squares will be created.

Input P takes a construction plane as input. Here, the default value is World XY, which is a plane that is defined in x- and y-direction and whose origin is has the coordinates 0,0,0. We get the same result, if we connect an XY Planeto input P.

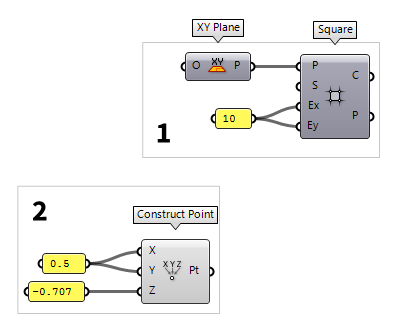
2

Define origin of bottom grid

Now that we have created one grid, we will create a second one that is offset to the first grid. To do this, we create a construction plane with a new point of origin; the component Construct Pointwill create this point with the coordinates that are given at the three inputs.

The horizontal offset of the grids is half of the cell size. Therefore, we create a Panelwith the value 0.5 and connect it to the inputs X and Y of Construct Point. The vertical offset is $h = 0.707$ and the second grid should be below the first one. Accordingly, we create another Panelwith -0.707 and connect it to input Z.

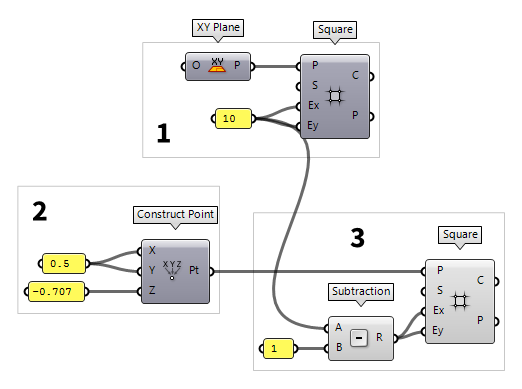
3

Generate bottom grid

The second grid is also created with the component Square. As mentioned above, input P takes a construction plane. What is left to do now, is to connect the just created point with input P. You may have noticed that we connected a point to an input which actually requests a plane. Grasshopper is sometimes smart and guesses missing information. In this case, it took the default World XY and altered the point of origin to the one we connected. If we need a plane in other directions then XY, we have to create the plane first and then hook it up.

If we take a look at the Rhino viewport, we notice that the symmetry of the grids has been lost due to the offset. For our space frame roof, we want the lower grid to be one cell less in each direction. In this case the desired number of cells is 9. But, we should solve this in a flexible manner: it’s one less than the initial number of cells. In Grasshopper, this translates to using a Subtractioncomponent and connecting the initial value to input A. At input B, we need a Panel with 1 (use Canvas search with "1). Now we connect output R of Subtraction with the inputs Ex and Ey of the second grid.

Show Rhino Show Grasshopper

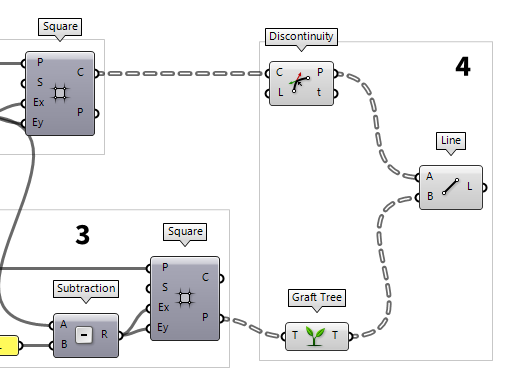
4

Generate the diagonals

The component Squarehas two outputs: At S we get the outlines of the cells, in this case squares, and at P we get the points at the grid corners. The data is arranged in data tree structure: Each branch represents a row of the grid and contains a list of squares or points.

We create the diagonals of the space frame by connecting the points of the upper grid with those of the lower grid. Such a connection can be created with the component Line. The big question is how to sort the points for the inputs A and B to create the desired connections. Let’s think of an half-octahedron (which is a pyramid) in isolation: It has a square base and an apex. The sloping edges connect the vertices of the base with the apex. The edges represent the diagonals that we are looking for. So we keep in mind: There are four vertices opposed by one vertex.

The edges of the base are the grid cell outlines at output C of Square. We can use the component Discontinuityto generate points at all kinks of the outlines; connect output C with input C. We now have the four vertices for the base. If we take a closer look at output P, we notice that the points are sorted as a data tree, whose last ramifications contains the 4 vertices of each grid cell as a list.

Now, we have the four base vertices but the counterpart, the apex, is still missing. It’s important that the apex needs do be in the same data tree structure as our base vertices: the last ramification should contain a list with only a single vertex. In this case, we need to use the component Graft Treein combination with the grid corners of the lower grid: Run a wire from output P of the lower grid to the input T which grafts our data tree. We then connect both data trees with the component Lineto generate the diagonals of our space frame.

Show Rhino Show Grasshopper

5

Construct tubes

The last step is to turn the axes into tubes. For this, we split the outlines of our cells (squares) into individual lines; the component Explodewill do this for us. Also, let’s not mind the doublicate lines that are caused by adjacent cells. At output S of Explode we find the separated lines and connect them together with the diagonals to input C of a Pipecomponent. To connect multiple wires to one input, keep holding Shift while connecting the wires. To define a radius for the pipes, we use a Panelwith 0.05 and connect it to input R. This will give our space frame roof some volume for a better visualization.

Show Rhino Show Grasshopper

Test your skills

As it’s often the case with writing algorithms, there are several ways to get the same solution. In this case, instead of using two square grids and connecting their vertices, the space frame roof could also be generated by creating the appropriate polyhedra and using their edges for the space frame. This is now your task! (Remember the reference to the pyramid?)

Hint 2

Generate the squares

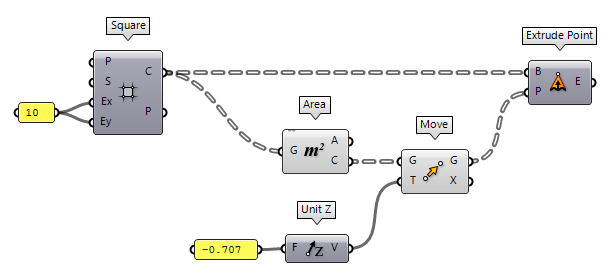
The squares are created with the component Square, just as in the main exercise. In order for Extrude Pointto work, we still need the apices of the pyramids.

Hint 3

Create the apices

For the apices, we use the component Areato find the center of each grid cell and then we use Moveto move them onto the other plane. Move requires a translation vector, which we get with the component Unit Z. Now we have pyramids (Breps) and only the axes for the tubes are missing.

Hint 4

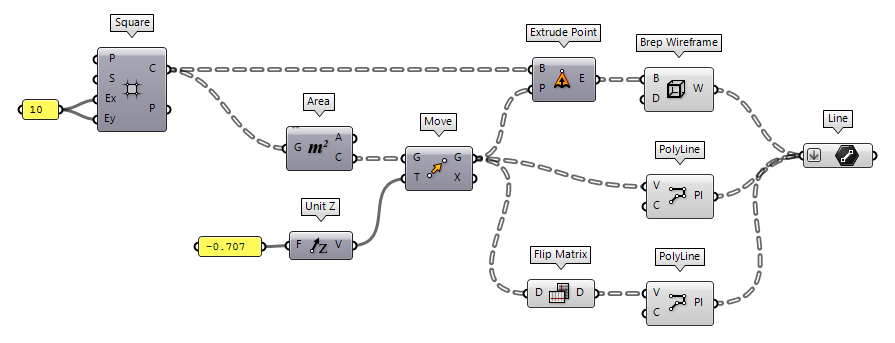
Find all lines of the space frame

The component Brep Wireframewill export the upper grid and the diagonals from the extruded Breps. For the lower grid we have to take a small detour via PolyLineand connect it with the moved points. Since this only gives us one direction of the lower grid, we use PolyLineagain, but this time we place a Flip Matrixcomponent in front of it.