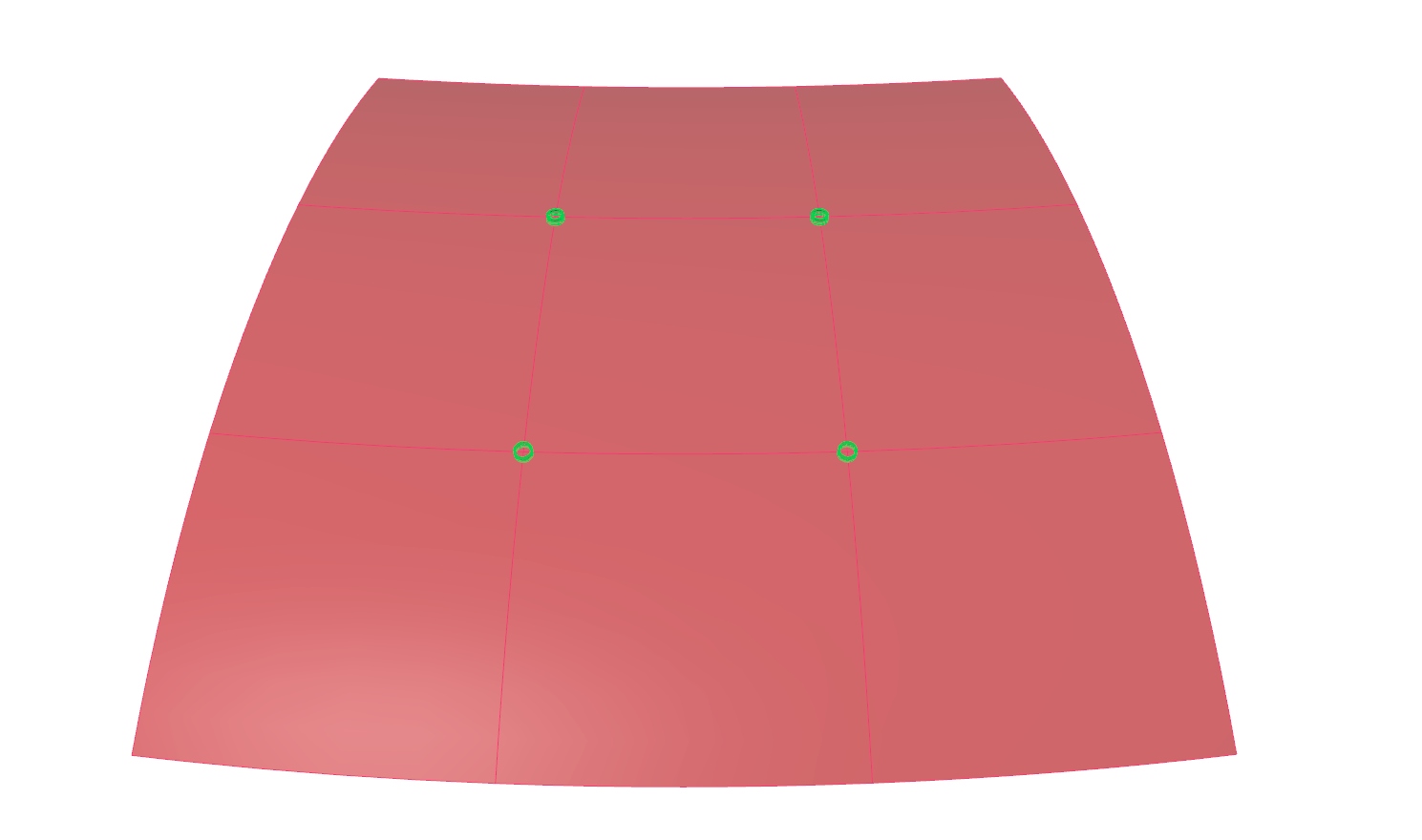
In this tutorial, we will model a joint in reference to one of a gridshell. Considerations of proper engineering are left out and the focus is solely on creating solids that are generated on aligned construction planes.
Operations on solids, like trimming or merging, are computationally intensive and will lock Grasshopper when parameters are changed upstream. Thus, the number of objects operated on should be limited. In this tutorial, this is done by creating a box that can be moved around and only the nodes inside the box are calculated.
Grasshopper
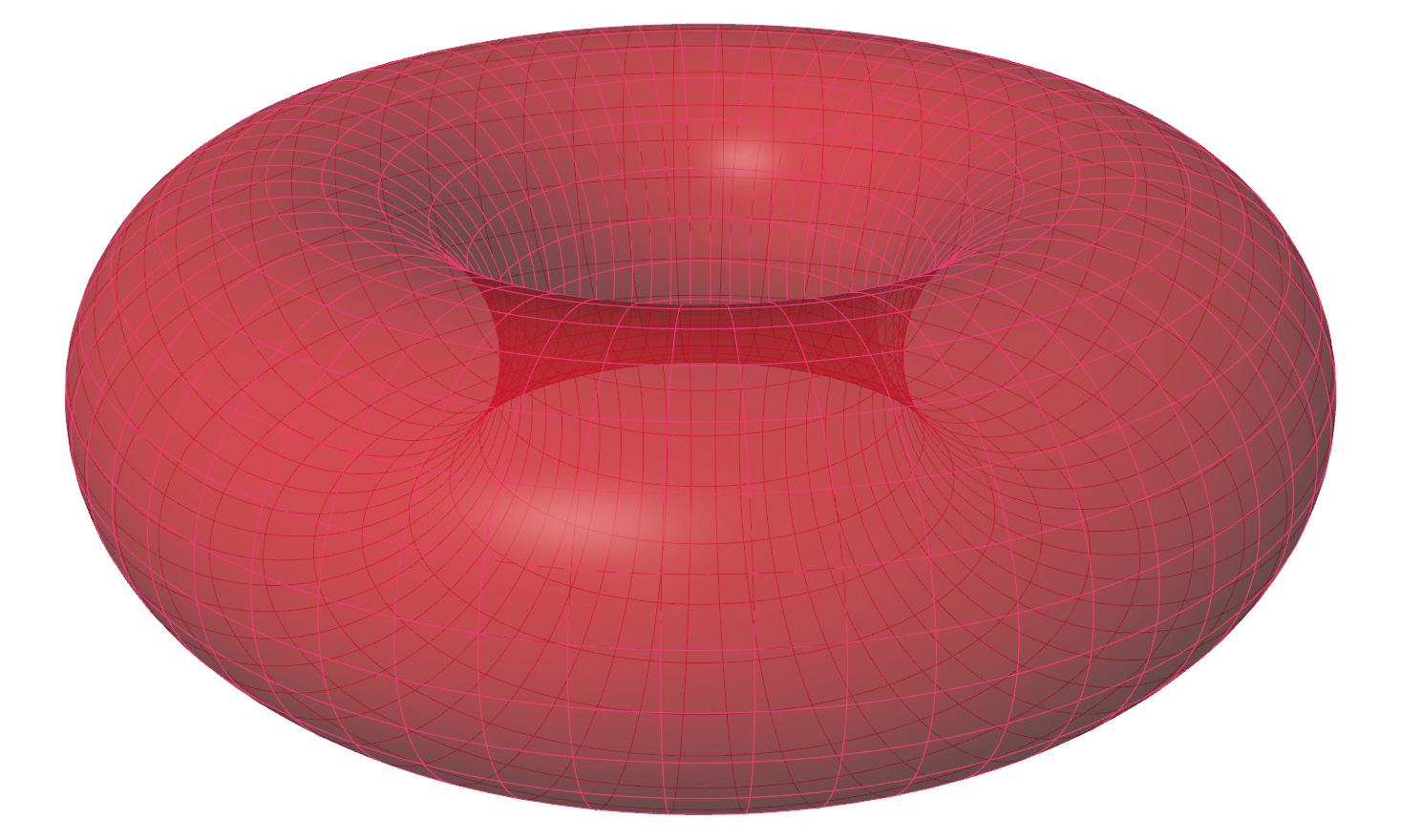
The methods described in this tutorial expect that a surface for the gridshell is present and that there are segmented surfaces for each grid cell. To keep it simple, we will use a torus hereafter.
0
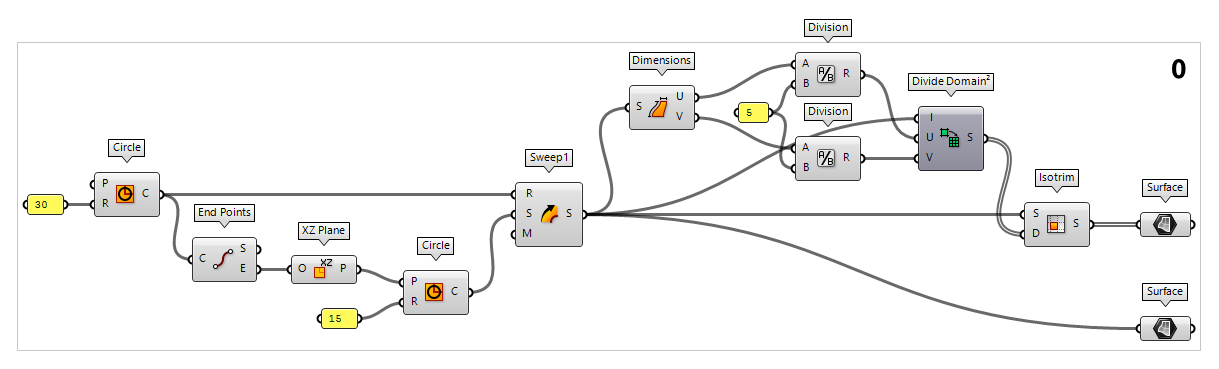
Generate a gridshell surface and subdivide it
To generate a torus as base geometry, we create a Circle Circle (Cir)
Circle (Cir)Inputs Plane (P) Base plane of circle Radius (R) Radius of circle Outputs Circle (C) Resulting circle 30 and then use End Points End Points (End)
End Points (End)Inputs Curve (C) Curve to evaluate Outputs Start (S) Curve start point End (E) Curve end point  XZ Plane (XZ)
XZ Plane (XZ)Inputs Origin (O) Origin of plane Outputs Plane (P) World XZ plane 15 and then use it as a section curve for Sweep1 Sweep1 (Swp1)
Sweep1 (Swp1)Inputs Rail (R) Rail curve Sections (S) Section curves Miter (M) Kink miter type (0=None, 1=Trim, 2=Rotate) Outputs Brep (S) Resulting Brep
To subdivide the surface of the torus, we first have to calculate the size of
the grid cells. We do this with Dimensions Dimensions (Dim)
Dimensions (Dim)Inputs Surface (S) Surface to measure Outputs U dimension (U) Approximate dimension in U direction V dimension (V) Approximate dimension in V direction  Division (A/B)
Division (A/B)Inputs A (A) Item to divide (dividend) B (B) Item to divide with (divisor) Outputs Result (R) The result of the Division 5 to get corresponding values. The component Divide Domain² Divide Domain² (Divide)
Divide Domain² (Divide)Inputs Domain (I) Base domain U Count (U) Number of segments in {u} direction V Count (V) Number of segments in {v} direction Outputs Segments (S) Individual segments  Isotrim (SubSrf)
Isotrim (SubSrf)Inputs Surface (S) Base surface Domain (D) Domain of subset Outputs Surface (S) Subset of base surface
1
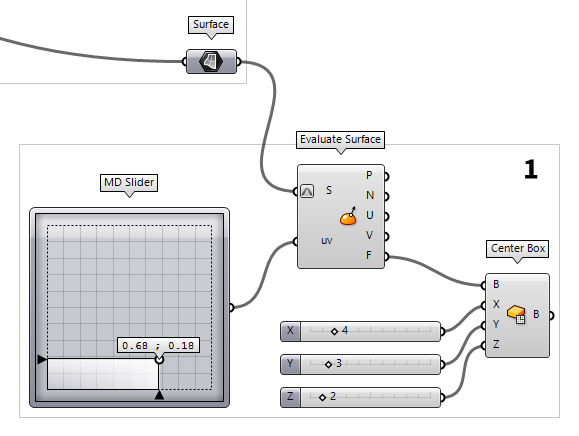
Create a box to capture nodes with
To place a box on the surface of the torus, we have to find the coordinates for
the box' base first. This is done with the component Evaluate Surface Evaluate Surface (EvalSrf)
Evaluate Surface (EvalSrf)Inputs Surface (S) Base surface Point (uv) {uv} coordinate to evaluate Outputs Point (P) Point at {uv} Normal (N) Normal at {uv} U direction (U) U direction at {uv} V direction (V) V direction at {uv} Frame (F) Frame at {uv}  MD Slider (MD Slider)
MD Slider (MD Slider) Center Box (Box)
Center Box (Box)Inputs Base (B) Base plane X (X) Size of box in {x} direction. Y (Y) Size of box in {y} direction. Z (Z) Size of box in {z} direction. Outputs Box (B) Resulting box  Number Slider
Number Slider
2
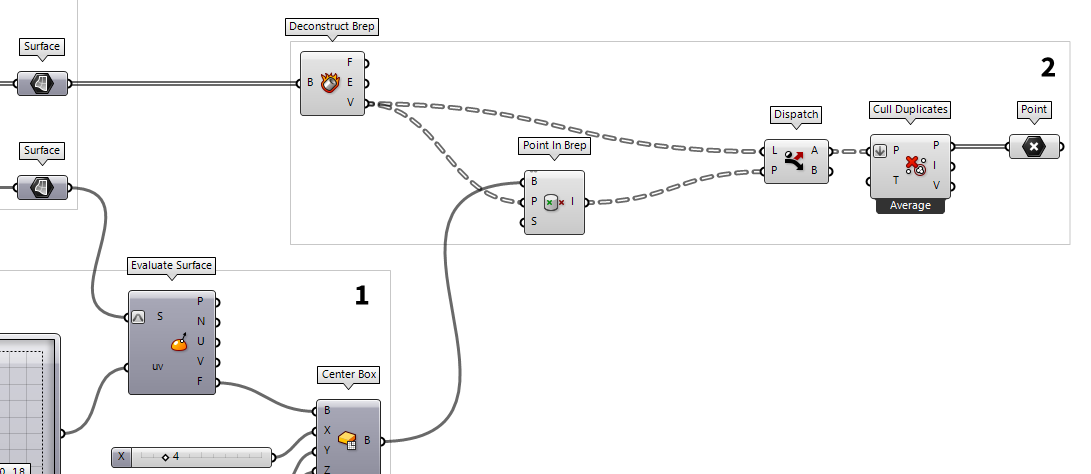
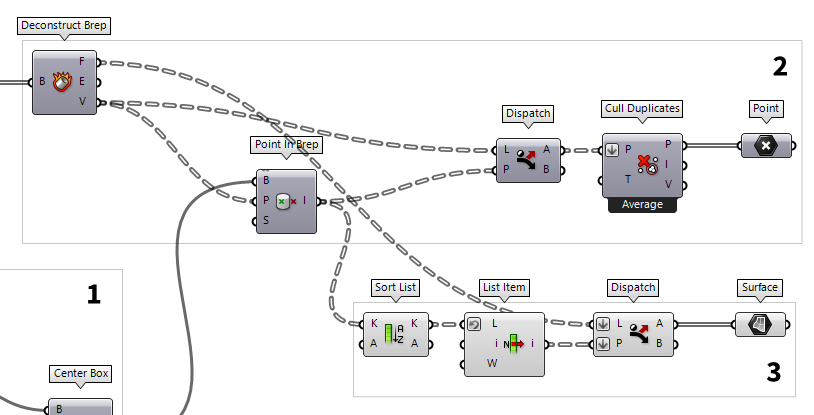
Isolate the captured nodes
To continue, we will further dismantle the grid cell surfaces with Deconstruct Brep Deconstruct Brep (DeBrep)
Deconstruct Brep (DeBrep)Inputs Brep (B) Base Brep Outputs Faces (F) Faces of Brep Edges (E) Edges of Brep Vertices (V) Vertices of Brep  Point In Brep (BrepInc)
Point In Brep (BrepInc)Inputs Brep (B) Brep for inclusion test Point (P) Point for inclusion test Strict (S) If true, then the inclusion is strict Outputs Inside (I) True if point is on the inside of the Brep.  Dispatch (Dispatch)
Dispatch (Dispatch)Inputs List (L) List to filter Dispatch pattern (P) Dispatch pattern Outputs List A (A) Dispatch target for True values List B (B) Dispatch target for False values
We now have all the nodes but the surfaces, that are next to each other, share
the same vertices. Thus, by dismantling the surfaces, we got vertices that have
the same coordinates as vertices from an adjacent surface. Thus, we use Cull Duplicates Cull Duplicates (CullPt)
Cull Duplicates (CullPt)Inputs Points (P) Points to operate on Tolerance (T) Proximity tolerance distance Outputs Points (P) Culled points Indices (I) Index map of culled points Valence (V) Number of input points represented by this output point
3
Select the surrounding surfaces
Next, we select the surfaces that connect to the identified nodes. The vertices
of each grid cell are separated in lists and this will help us to get the right
surfaces. We connect a Sort List Sort List (Sort)
Sort List (Sort)Inputs Keys (K) List of sortable keys Values A (A) Optional list of values to sort synchronously Outputs Keys (K) Sorted keys Values A (A) Synchronous values in A  Point In Brep (BrepInc)
Point In Brep (BrepInc)Inputs Brep (B) Brep for inclusion test Point (P) Point for inclusion test Strict (S) If true, then the inclusion is strict Outputs Inside (I) True if point is on the inside of the Brep.  List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'} 1 for True is forwarded. Using Dispatch Dispatch (Dispatch)
Dispatch (Dispatch)Inputs List (L) List to filter Dispatch pattern (P) Dispatch pattern Outputs List A (A) Dispatch target for True values List B (B) Dispatch target for False values
4
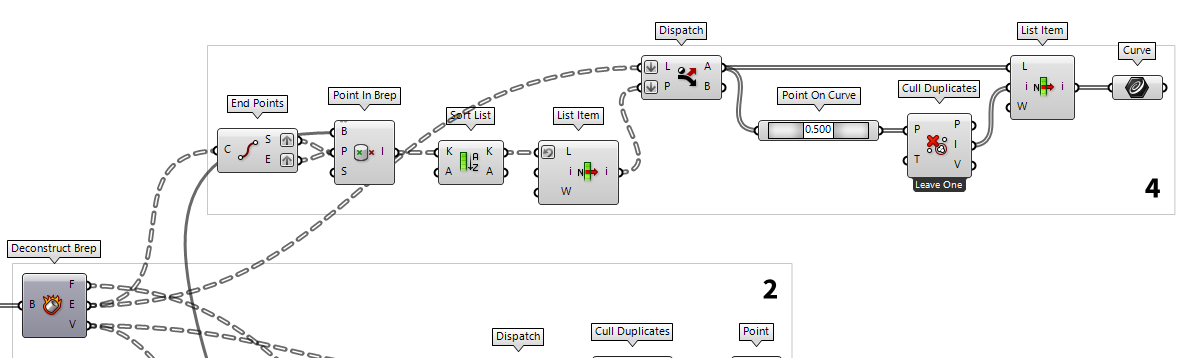
Select the connected curves
To find the curves which are connected to the nodes, we grab the edges E
from the dismantled grid cells and attach an End Points End Points (End)
End Points (End)Inputs Curve (C) Curve to evaluate Outputs Start (S) Curve start point End (E) Curve end point  Point In Brep (BrepInc)
Point In Brep (BrepInc)Inputs Brep (B) Brep for inclusion test Point (P) Point for inclusion test Strict (S) If true, then the inclusion is strict Outputs Inside (I) True if point is on the inside of the Brep.  Sort List (Sort)
Sort List (Sort)Inputs Keys (K) List of sortable keys Values A (A) Optional list of values to sort synchronously Outputs Keys (K) Sorted keys Values A (A) Synchronous values in A  List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'} 1
for True to a Dispatch Dispatch (Dispatch)
Dispatch (Dispatch)Inputs List (L) List to filter Dispatch pattern (P) Dispatch pattern Outputs List A (A) Dispatch target for True values List B (B) Dispatch target for False values
We now have all the edges that are completely or partially in the box, but
because adjacent cells have equal edges, there are some duplicate ones. We can
remove duplicate curves by getting
their midpoint as a Point On Curve Point On Curve (CurvePoint)
Point On Curve (CurvePoint) Cull Duplicates (CullPt)
Cull Duplicates (CullPt)Inputs Points (P) Points to operate on Tolerance (T) Proximity tolerance distance Outputs Points (P) Culled points Indices (I) Index map of culled points Valence (V) Number of input points represented by this output point  Cull Duplicates (CullPt)
Cull Duplicates (CullPt)Inputs Points (P) Points to operate on Tolerance (T) Proximity tolerance distance Outputs Points (P) Culled points Indices (I) Index map of culled points Valence (V) Number of input points represented by this output point  List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'}
5
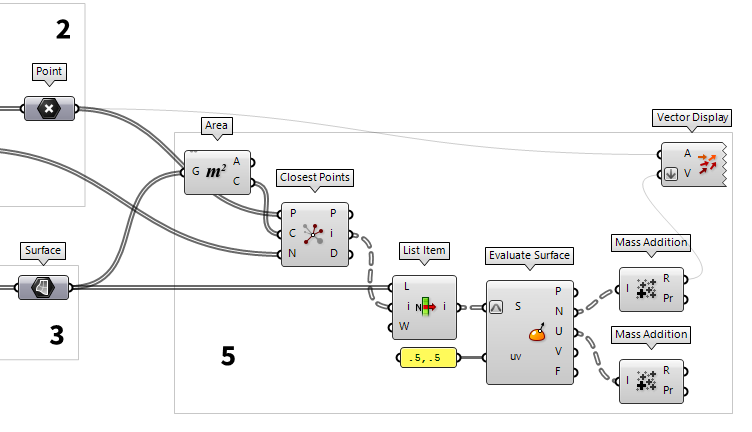
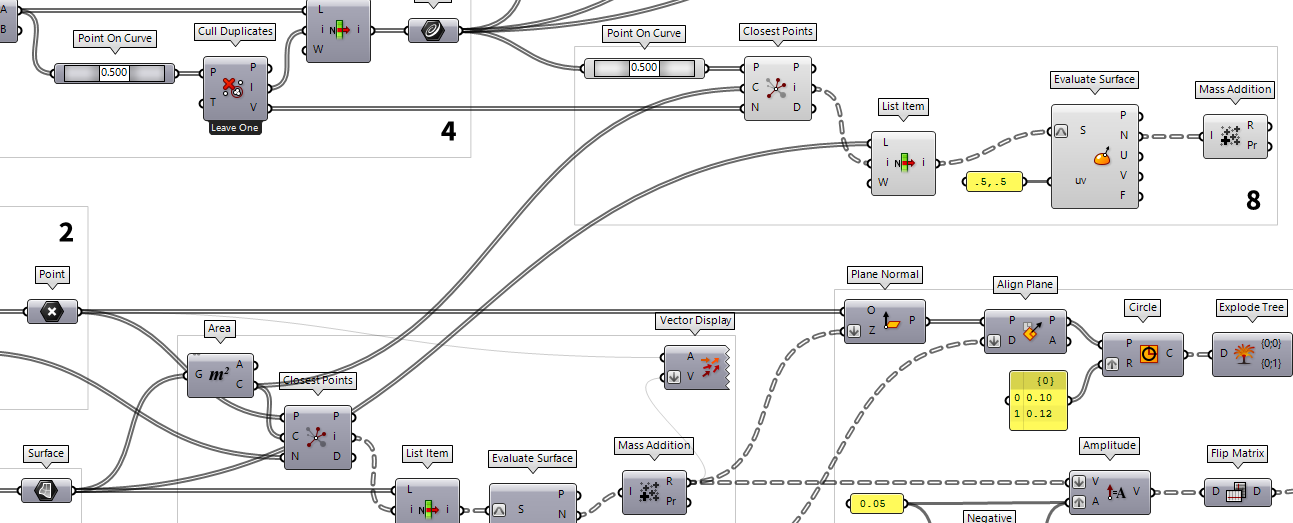
Find proper vectors for construction planes
All cells of the gridshell have a different orientation in space and the construction planes of the joints should deviate as little as possible from the adjacent surfaces. For this, we calculate the mean vector by adding the normal vectors of the corresponding cells.
Before we can add the vectors, we have to find the cells that are associated
with a node. For this, we use Area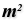 Area (Area)
Area (Area)Inputs Geometry (G) Brep, mesh or planar closed curve for area computation Outputs Area (A) Area of geometry Centroid (C) Area centroid of geometry  Closest Points (CPs)
Closest Points (CPs)Inputs Point (P) Point to search from Cloud (C) Cloud of points to search Count (N) Number of closest points to find Outputs Closest Point (P) Point in [C] closest to [P] CP Index (i) Index of closest point Distance (D) Distance between [P] and [C](i)  Cull Duplicates (CullPt)
Cull Duplicates (CullPt)Inputs Points (P) Points to operate on Tolerance (T) Proximity tolerance distance Outputs Points (P) Culled points Indices (I) Index map of culled points Valence (V) Number of input points represented by this output point
We now have a separate list of associated surface indices for each node and a
List Item List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'}  Evaluate Surface (EvalSrf)
Evaluate Surface (EvalSrf)Inputs Surface (S) Base surface Point (uv) {uv} coordinate to evaluate Outputs Point (P) Point at {uv} Normal (N) Normal at {uv} U direction (U) U direction at {uv} V direction (V) V direction at {uv} Frame (F) Frame at {uv}  Panel
Panel.5,.5 will evaluate the surface at its center. At output
N we get the normal vectors and we add them with Mass Addition Mass Addition (MA)
Mass Addition (MA)Inputs Input (I) Input values for mass addition. Outputs Result (R) Result of mass addition Partial Results (Pr) List of partial results  Mass Addition (MA)
Mass Addition (MA)Inputs Input (I) Input values for mass addition. Outputs Result (R) Result of mass addition Partial Results (Pr) List of partial results
6
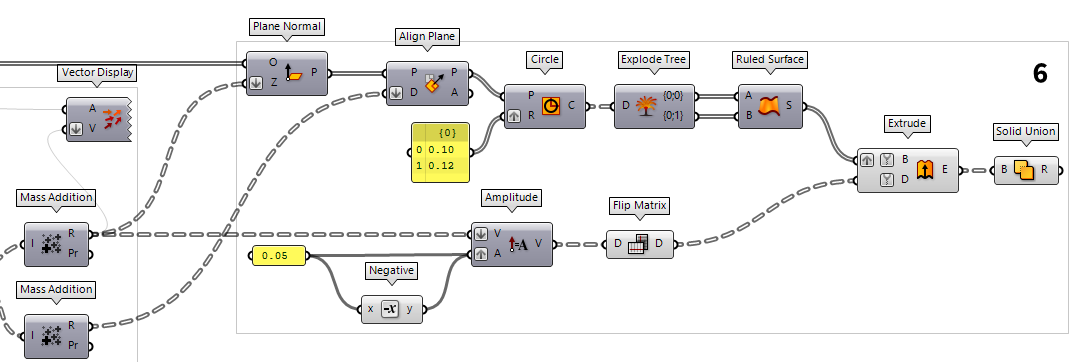
Create solids for joints
The next task is to create the construction planes
with the just created vectors: First we create planes perpendicular to the mean
normal vectors with Plane Normal Plane Normal (Pl)
Plane Normal (Pl)Inputs Origin (O) Origin of plane Z-Axis (Z) Z-Axis direction of plane Outputs Plane (P) Plane definition  Align Plane (Align)
Align Plane (Align)Inputs Plane (P) Plane to straighten Direction (D) Straightening guide direction Outputs Plane (P) Straightened plane Angle (A) Rotation angle
Now that we have our construction planes, we will create a ring that the grid
members can later attach to. In a Panel Panel
Panel0.10 and
0.12) and draw matching circles with Circle Circle (Cir)
Circle (Cir)Inputs Plane (P) Base plane of circle Radius (R) Radius of circle Outputs Circle (C) Resulting circle  Explode Tree (BANG!)
Explode Tree (BANG!)Inputs Data (D) Data to explode Outputs Branch 0 (-) All data inside the branch at index: 0 Branch 1 (-) All data inside the branch at index: 1  Ruled Surface (RuleSrf)
Ruled Surface (RuleSrf)Inputs Curve A (A) First curve Curve B (B) Second curve Outputs Surface (S) Ruled surface between A and B
The axes of the grid members will meet the ring at half height, so we have to
extrude it upwards and downwards. The direction of the extrusion vectors is
given by the mean normal vectors and we have to adjust their length. A panel
with 0.05 will give us a value for half of the height and Negative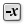 Negative (Neg)
Negative (Neg)Inputs Value (x) Input value Outputs Result (y) Output value  Amplitude (Amp)
Amplitude (Amp)Inputs Vector (V) Base vector Amplitude (A) Amplitude (length) value Outputs Vector (V) Resulting vector  Flip Matrix (Flip)
Flip Matrix (Flip)Inputs Data (D) Data matrix to flip Outputs Data (D) Flipped data matrix
To put it all together, we use an Extrude Extrude (Extr)
Extrude (Extr)Inputs Base (B) Profile curve or surface Direction (D) Extrusion direction Outputs Extrusion (E) Extrusion result  Solid Union (SUnion)
Solid Union (SUnion)Inputs Breps (B) Breps to union Outputs Result (R) Union result
7
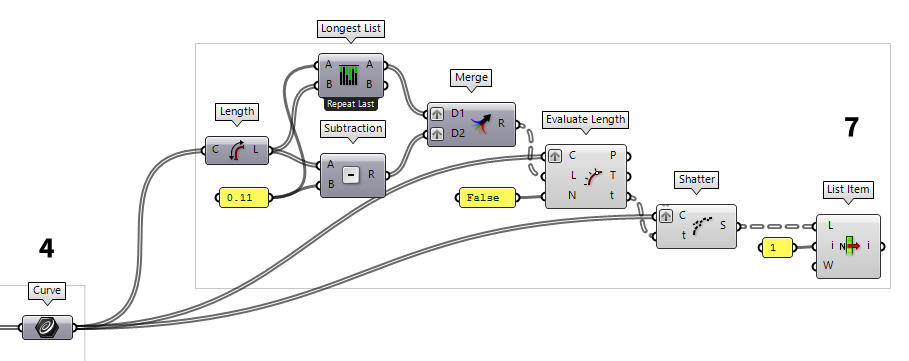
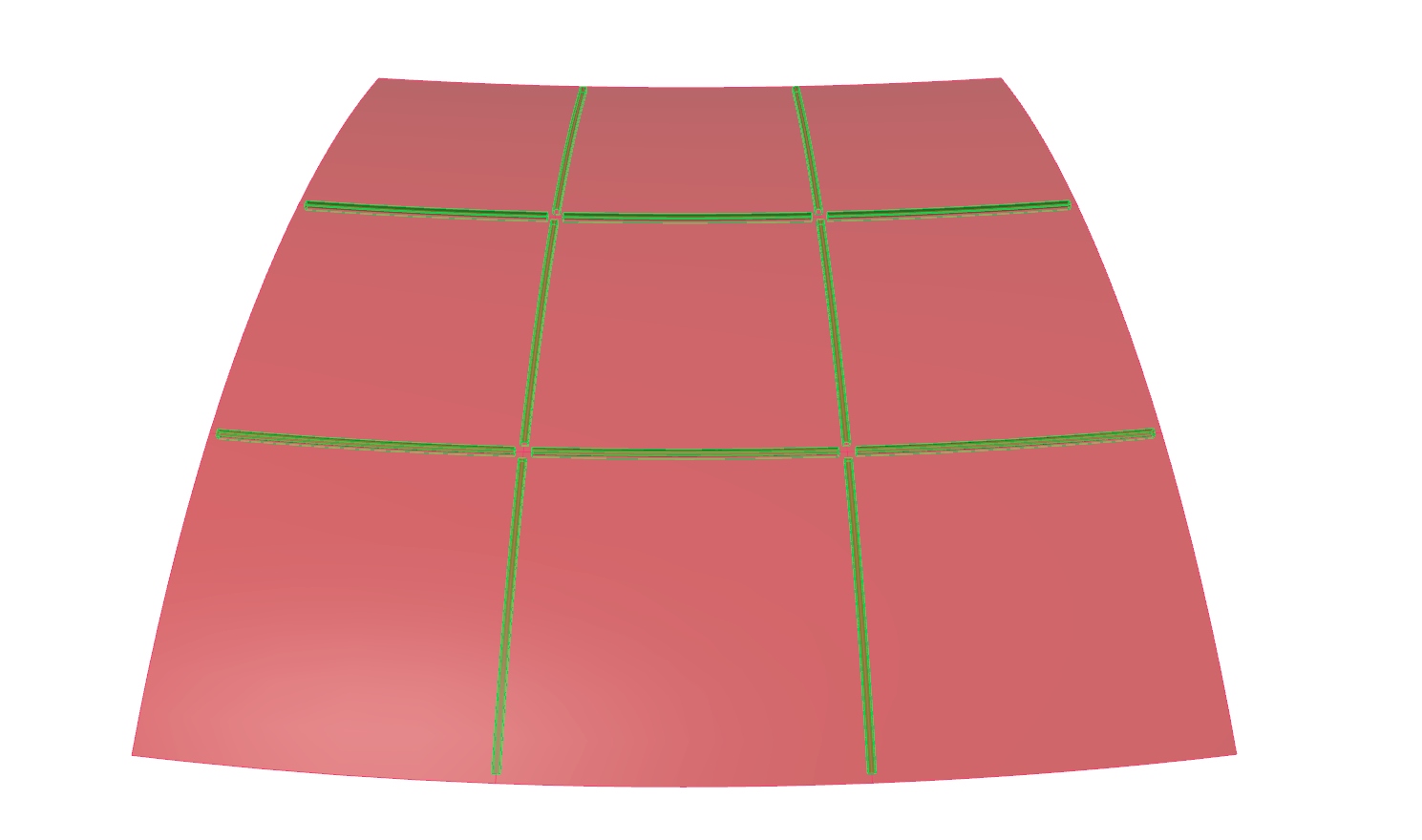
Shorten length of grid members
We will continue with the curves from step 4. The goal is to shorten them, so
that they end on the center lines of the rings. In this example, we will cut off
0.11 from each end. After retrieving their initial Length Length (Len)
Length (Len)Inputs Curve (C) Curve to measure Outputs Length (L) Curve length  Subtraction (A-B)
Subtraction (A-B)Inputs A (A) First operand for subtraction B (B) Second operand for subtraction Outputs Result (R) Result of subtraction 0.11. But we need this value for each line. Thus, we
have to use Longest List Longest List (Long)
Longest List (Long)Inputs List (A) (A) List (A) to operate on List (B) (B) List (B) to operate on Outputs List (A) (A) Adjusted list (A) List (B) (B) Adjusted list (B)  Merge (Merge)
Merge (Merge)Inputs Data 1 (D1) Data stream 1 Data 2 (D2) Data stream 2 Outputs Result (R) Result of merge
To shatter the curves at these lengths, we have to calculate their curve parameters. For
this, we use Evaluate Length Evaluate Length (Eval)
Evaluate Length (Eval)Inputs Curve (C) Curve to evaluate Length (L) Length factor for curve evaluation Normalized (N) If True, the Length factor is normalized (0.0 ~ 1.0) Outputs Point (P) Point at the specified length Tangent (T) Tangent vector at the specified length Parameter (t) Curve parameter at the specified length 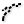 Shatter (Shatter)
Shatter (Shatter)Inputs Curve (C) Curve to trim Parameters (t) Parameters to split at Outputs Segments (S) Shattered remains  List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'} 1. We now
find the shortened curves at its output.
8
Calculate vectors for construction planes
To create a section profile for each curve, we have to generate a construction plane. This should deviate as little as possible from the neighboring cells, so that the grid member has the same tilt to both adjacent surfaces (similar to step 5).
With Point On Curve Point On Curve (CurvePoint)
Point On Curve (CurvePoint) Closest Points (CPs)
Closest Points (CPs)Inputs Point (P) Point to search from Cloud (C) Cloud of points to search Count (N) Number of closest points to find Outputs Closest Point (P) Point in [C] closest to [P] CP Index (i) Index of closest point Distance (D) Distance between [P] and [C](i)  Cull Duplicates (CullPt)
Cull Duplicates (CullPt)Inputs Points (P) Points to operate on Tolerance (T) Proximity tolerance distance Outputs Points (P) Culled points Indices (I) Index map of culled points Valence (V) Number of input points represented by this output point  Evaluate Surface (EvalSrf)
Evaluate Surface (EvalSrf)Inputs Surface (S) Base surface Point (uv) {uv} coordinate to evaluate Outputs Point (P) Point at {uv} Normal (N) Normal at {uv} U direction (U) U direction at {uv} V direction (V) V direction at {uv} Frame (F) Frame at {uv} .5,.5 as uv-coordinate and calculate
the mean vector with Mass Addition Mass Addition (MA)
Mass Addition (MA)Inputs Input (I) Input values for mass addition. Outputs Result (R) Result of mass addition Partial Results (Pr) List of partial results
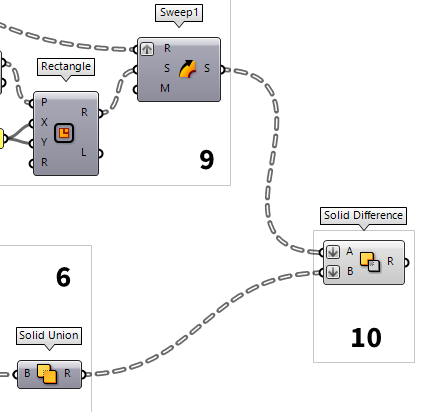
9
Create solids for grid members
Next, we will give body to the grid members. By using Perp Frame Perp Frame (PFrame)
Perp Frame (PFrame)Inputs Curve (C) Curve to evaluate Parameter (t) Parameter on curve domain to evaluate Outputs Frame (F) Perpendicular curve frame at {t} 0. These planes are not yet aligned with our surfaces and we need
to use Align Plane Align Plane (Align)
Align Plane (Align)Inputs Plane (P) Plane to straighten Direction (D) Straightening guide direction Outputs Plane (P) Straightened plane Angle (A) Rotation angle
The actual section profile is drawn as a Rectangle Rectangle (Rectangle)
Rectangle (Rectangle)Inputs Plane (P) Rectangle base plane X Size (X) Dimensions of rectangle in plane X direction. Y Size (Y) Dimensions of rectangle in plane Y direction. Radius (R) Rectangle corner fillet radius Outputs Rectangle (R) Rectangle Length (L) Length of rectangle curve -0.045 To 0.045. This way, our curves remains
the axes of our members. We then use Sweep1 Sweep1 (Swp1)
Sweep1 (Swp1)Inputs Rail (R) Rail curve Sections (S) Section curves Miter (M) Kink miter type (0=None, 1=Trim, 2=Rotate) Outputs Brep (S) Resulting Brep
10
Solve intersection for joints and grid members
In the steps before, we have created joints and grid members as solids, but they
still interpenetrate. We can now either trim the joints with the grid members or
the grid members with the joints by using the Solid Difference Solid Difference (SDiff)
Solid Difference (SDiff)Inputs Breps A (A) First Brep set Breps B (B) Second Brep set Outputs Result (R) Difference result
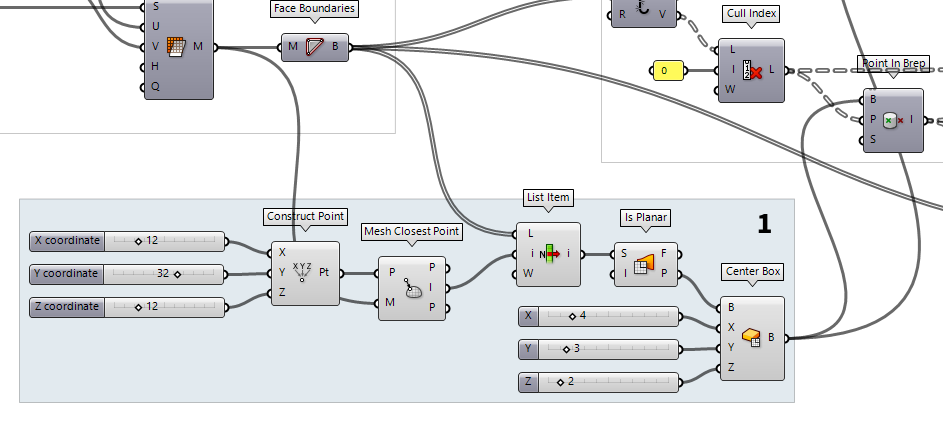
But I only have a mesh…
Let’s have a look at what has to be changed, if we initially started with a mesh
instead of a surface. To quickly create a mesh, we use Mesh Surface Mesh Surface (Mesh UV)
Mesh Surface (Mesh UV)Inputs Surface (S) Surface geometry U Count (U) Number of quads in U direction V Count (V) Number of quads in V direction Overhang (H) Allow faces to overhang trims Equalize (Q) Equalize span length Outputs Mesh (M) UV Mesh  Face Boundaries (FaceB)
Face Boundaries (FaceB)Inputs Mesh (M) Mesh for face boundary extraction Outputs Boundaries (B) Boundary polylines for each mesh face
To rework step 1 (creating the capture box), we have to do a little more work to
find a replacement for Evaluate Surface Evaluate Surface (EvalSrf)
Evaluate Surface (EvalSrf)Inputs Surface (S) Base surface Point (uv) {uv} coordinate to evaluate Outputs Point (P) Point at {uv} Normal (N) Normal at {uv} U direction (U) U direction at {uv} V direction (V) V direction at {uv} Frame (F) Frame at {uv}  Construct Point (Pt)
Construct Point (Pt)Inputs X coordinate (X) {x} coordinate Y coordinate (Y) {y} coordinate Z coordinate (Z) {z} coordinate Outputs Point (Pt) Point coordinate  Mesh Closest Point (MeshCP)
Mesh Closest Point (MeshCP)Inputs Point (P) Point to search from Mesh (M) Mesh to search for closest point Outputs Point (P) Location on mesh closest to search point Index (I) Face index of closest point Parameter (P) Mesh parameter for closest point  List Item (Item)
List Item (Item)Inputs List (L) Base list Index (i) Item index Wrap (W) Wrap index to list bounds Outputs Item (i) Item at {i'}  Face Boundaries (FaceB)
Face Boundaries (FaceB)Inputs Mesh (M) Mesh for face boundary extraction Outputs Boundaries (B) Boundary polylines for each mesh face
To create a construction plane for our box, we use Is Planar Is Planar (Planar)
Is Planar (Planar)Inputs Surface (S) Surface to test for planarity Interior (I) Limit planarity test to the interior of trimmed surfaces Outputs Planar (F) Planarity flag of surface Plane (P) Surface plane
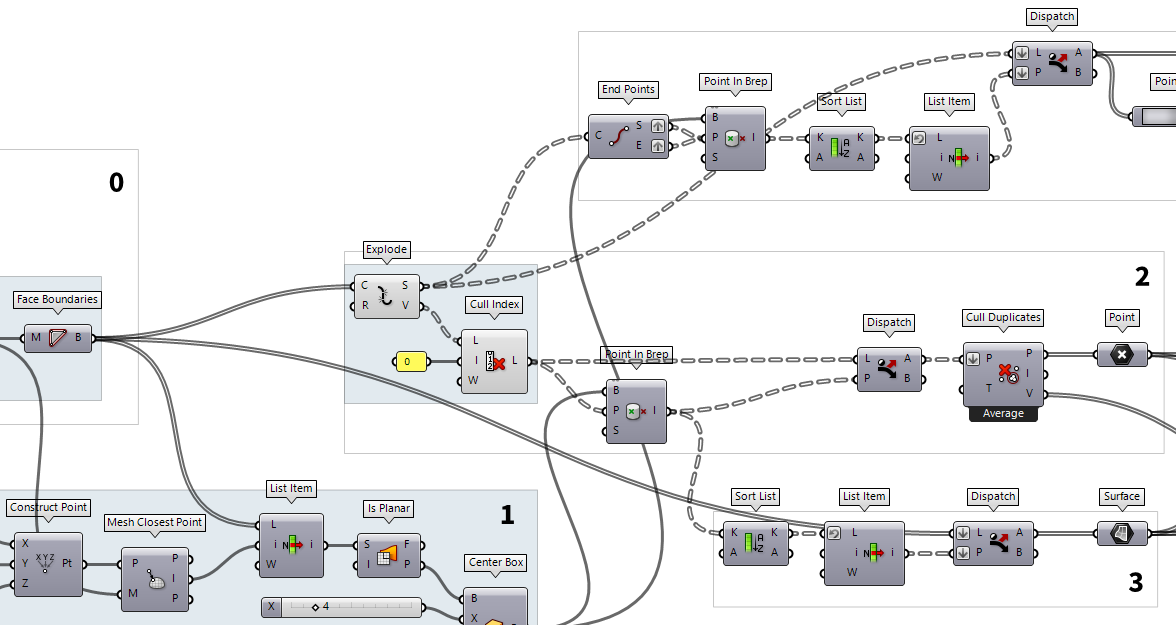
What remains, is to find a substitution for Deconstruct Brep Deconstruct Brep (DeBrep)
Deconstruct Brep (DeBrep)Inputs Brep (B) Base Brep Outputs Faces (F) Faces of Brep Edges (E) Edges of Brep Vertices (V) Vertices of Brep  Surface (Srf)
Surface (Srf) Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments  Explode (Explode)
Explode (Explode)Inputs Curve (C) Curve to explode Recursive (R) Recursive decomposition until all segments are atomic Outputs Segments (S) Exploded segments that make up the base curve Vertices (V) Vertices of the exploded segments  Cull Index (Cull i)
Cull Index (Cull i)Inputs List (L) List to cull Indices (I) Culling indices Wrap (W) Wrap indices to list range Outputs List (L) Culled list
Now, every change is made to use the algorithm with meshes. It could be tweaked even more to use mesh faces for the calculation of the construction plane vectors. This optimization would be even more useful if additional Grasshopper Plugins would be used. For now, it’s fine for vanilla Grasshopper.