This how-to guide is focusing on domains and the various components and component compositions that host valuable functions related to domains. In mathematics, a domain refers to the input values of a function and the range refers to the values that this function can output. In Grasshopper, both terms are often used indistinctly; a range can be a domain or a defined series of numbers. Domains are specified as a domain of numeric range. Despite this vague mathematical description, domains in Grasshopper are well-defined as a data type.
Domains in Grasshopper have defined bounds that are represented by a lower and a
upper value, like 0 and 1. Within the domain, all real numbers are possible
that exist between the bounds. A domain is written as 0 To 1. Beside this data
type Domain Domain (Domain)
Domain (Domain) Domain² (Domain²)
Domain² (Domain²)
Construct Domains
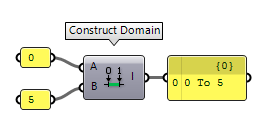
The most official way to construct a domain is using the component Construct Domain Construct Domain (Dom)
Construct Domain (Dom)Inputs Domain start (A) Start value of numeric domain Domain end (B) End value of numeric domain Outputs Domain (I) Numeric domain between {A} and {B}
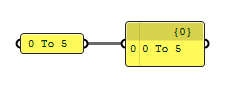
Another way is to use a Panel Panel
Panel0 To 5. Whenever a component requests for a domain, this string
format will be converted to one.
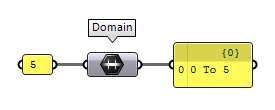
If a component requests a domain, but only a single number is provided, than this
number becomes the upper bound and the lower bound is set to 0, as demonstrated with
the Domain Domain (Domain)
Domain (Domain)
The component Bounds Bounds (Bnd)
Bounds (Bnd)Inputs Numbers (N) Numbers to include in Bounds Outputs Domain (I) Numeric Domain between the lowest and highest numbers in {N}
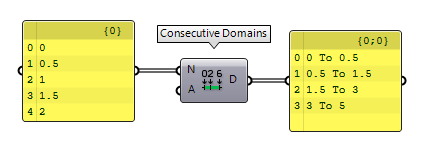
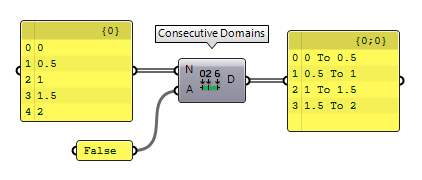
The component Consecutive Domains Consecutive Domains (Consec)
Consecutive Domains (Consec)Inputs Numbers (N) Numbers for consecutive domains Additive (A) If True, values are added to a sum-total Outputs Domains (D) Domains describing the spaces between the numbers
If we set input A of Consecutive Domains Consecutive Domains (Consec)
Consecutive Domains (Consec)Inputs Numbers (N) Numbers for consecutive domains Additive (A) If True, values are added to a sum-total Outputs Domains (D) Domains describing the spaces between the numbers
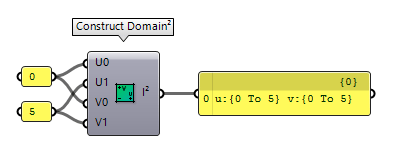
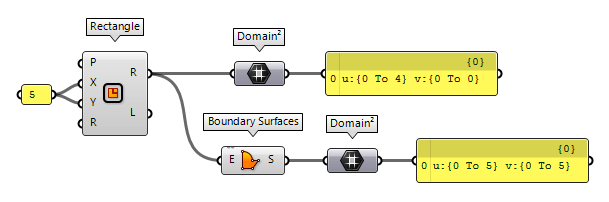
To construct the data type Domain², there are two possibilities. The first one
is to use Construct Domain² Construct Domain² (Dom²Num)
Construct Domain² (Dom²Num)Inputs U min (U0) Lower limit of domain in {u} direction U max (U1) Upper limit of domain in {u} direction V min (V0) Lower limit of domain in {v} direction V max (V1) Upper limit of domain in {v} direction Outputs 2D Domain (I²) Two dimensional numeric domain of {u} and {v}
The second possibility is to use Construct Domain² Construct Domain² (Dom²)
Construct Domain² (Dom²)Inputs Domain U (U) Domain in {u} direction Domain V (V) Domain in {v} direction Outputs 2D Domain (I²) Two dimensional numeric domain of {u} and {v}
Deconstruct domains
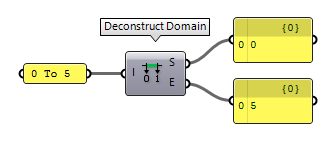
Of course, if domains can be constructed, they can also be deconstructed and Deconstruct Domain Deconstruct Domain (DeDomain)
Deconstruct Domain (DeDomain)Inputs Domain (I) Base domain Outputs Start (S) Start of domain End (E) End of domain
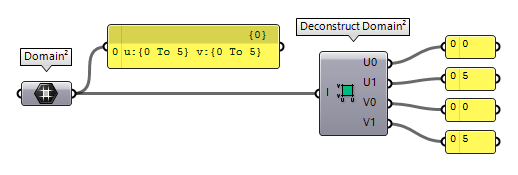
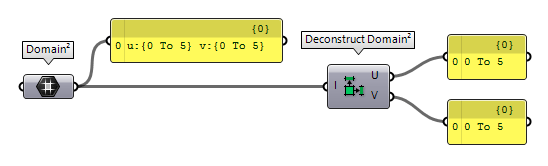
For the data type Domain², there are again two possibilities: The component
Deconstruct Domain² Deconstruct Domain² (DeDom2Num)
Deconstruct Domain² (DeDom2Num)Inputs Domain (I) Base domain Outputs U min (U0) Lower limit of domain in {u} direction U max (U1) Upper limit of domain in {u} direction V min (V0) Lower limit of domain in {v} direction V max (V1) Upper limit of domain in {v} direction
The alternative is Deconstruct Domain² Deconstruct Domain² (DeDom2)
Deconstruct Domain² (DeDom2)Inputs Domain (I) Base domain Outputs U component (U) {u} component of domain V component (V) {v} component of domain
Retrieve domains from geometric objects
Domains are often used in combination with geometric objects. At an object’s
input, we can use Reparameterize to rewrite the actual domain into a normalized one (0 To 1). Then we relate our operations to the normalized domain and do not need to
know the actual domain. This is useful, if the real bounds vary from
shape to shape.
If we need to retrieve the real domain of a geometric shape, we can also do
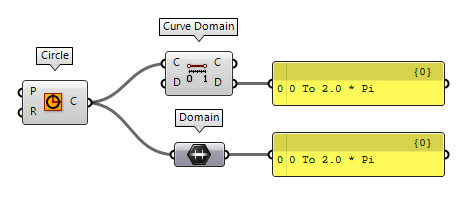
this. Curves have one direction and they translate into data type Domain. The
component Curve Domain Curve Domain (CrvDom)
Curve Domain (CrvDom)Inputs Curve (C) Curve to measure/modify Domain (D) Optional domain, if omitted the curve will not be modified. Outputs Curve (C) Curve with new domain. Domain (D) Domain of original curve.  Domain (Domain)
Domain (Domain) Curve Domain (CrvDom)
Curve Domain (CrvDom)Inputs Curve (C) Curve to measure/modify Domain (D) Optional domain, if omitted the curve will not be modified. Outputs Curve (C) Curve with new domain. Domain (D) Domain of original curve.  Domain (Domain)
Domain (Domain) Curve Domain (CrvDom)
Curve Domain (CrvDom)Inputs Curve (C) Curve to measure/modify Domain (D) Optional domain, if omitted the curve will not be modified. Outputs Curve (C) Curve with new domain. Domain (D) Domain of original curve.  Domain (Domain)
Domain (Domain)
A surface has two directions (u and v) and translates to data type
Domain². For retrieving, we can use a Domain² Domain² (Domain²)
Domain² (Domain²)
If we have a cloud of points, we can use Bounds 2D Bounds 2D (Bnd)
Bounds 2D (Bnd)Inputs Coordinates (C) Two dimensional coordinates to include in Bounds Outputs Domain (I) Numeric two-dimensional domain between the lowest and highest numbers in {N.x ; N.y}  Deconstruct (pDecon)
Deconstruct (pDecon)Inputs Point (P) Input point Outputs X component (X) Point {x} component Y component (Y) Point {y} component Z component (Z) Point {z} component  Bounds (Bnd)
Bounds (Bnd)Inputs Numbers (N) Numbers to include in Bounds Outputs Domain (I) Numeric Domain between the lowest and highest numbers in {N}
Divide domains
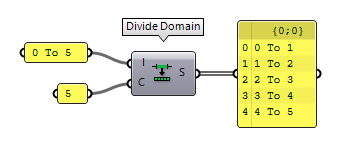
Because domains host a range of numbers, we can also subdivide them into
smaller units. The component Divide Domain Divide Domain (Div)
Divide Domain (Div)Inputs Domain (I) Base domain Count (C) Number of segments Outputs Segments (S) Division segments
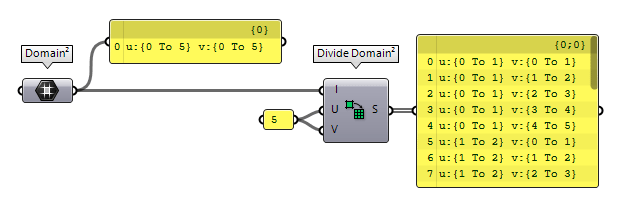
The component Divide Domain² Divide Domain² (Divide)
Divide Domain² (Divide)Inputs Domain (I) Base domain U Count (U) Number of segments in {u} direction V Count (V) Number of segments in {v} direction Outputs Segments (S) Individual segments
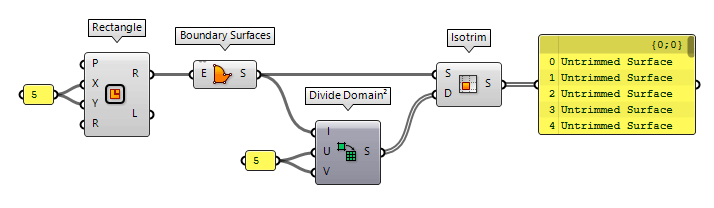
The operation Divide Domain² Divide Domain² (Divide)
Divide Domain² (Divide)Inputs Domain (I) Base domain U Count (U) Number of segments in {u} direction V Count (V) Number of segments in {v} direction Outputs Segments (S) Individual segments  Isotrim (SubSrf)
Isotrim (SubSrf)Inputs Surface (S) Base surface Domain (D) Domain of subset Outputs Surface (S) Subset of base surface
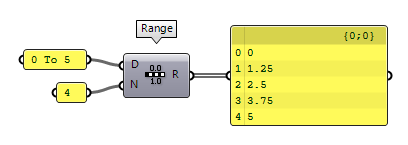
The component Range Range (Range)
Range (Range)Inputs Domain (D) Domain of numeric range Steps (N) Number of steps Outputs Range (R) Range of numbers
Remap a domain
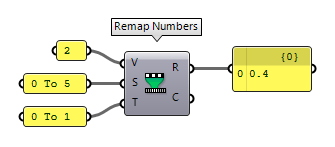
The component Remap Numbers Remap Numbers (ReMap)
Remap Numbers (ReMap)Inputs Value (V) Value to remap Source (S) Source domain Target (T) Target domain Outputs Mapped (R) Remapped number Clipped (C) Remapped and clipped number 0 To 1, we can use this component to
normalize numbers. See how-to Curve and surface parameters for more about
reparameterization.
Check domains
To test a number for its relation to one or more domains, there are two
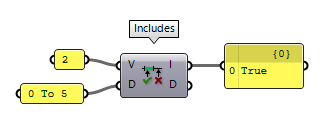
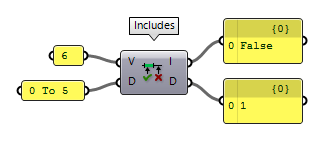
components present in Grasshopper. Includes Includes (Inc)
Includes (Inc)Inputs Value (V) Value to test for inclusion Domain (D) Domain to test with Outputs Includes (I) True if the value is included in the domain Deviation (D) Distance between the value and the nearest value inside the domain
In case that the number is not part of the domain, output D will state the distance between the given number and the nearest bound of the domain.
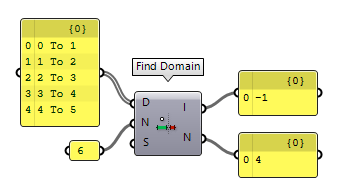
The component Find Domain Find Domain (FDom)
Find Domain (FDom)Inputs Domains (D) Collection of domains to search Number (N) Number to test Strict (S) Strict comparison, if true then the value must be on the interior of a domain Outputs Index (I) Index of first domain that includes the specified value Neighbour (N) Index of domain that is closest to the specified value
If the number is not part of any domain, then we can find the nearest domain at output N.
If we set input S (strict) of Find Domain Find Domain (FDom)
Find Domain (FDom)Inputs Domains (D) Collection of domains to search Number (N) Number to test Strict (S) Strict comparison, if true then the value must be on the interior of a domain Outputs Index (I) Index of first domain that includes the specified value Neighbour (N) Index of domain that is closest to the specified value True, the given
number N has to be part of the interior of the domain and can not be equal
to one of the bounds.