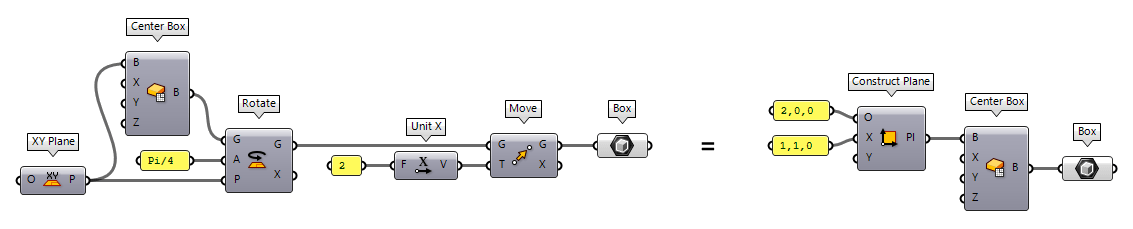
Everything we draw in Rhino or Grasshopper is part of a global Cartesian coordinate system, also called the world coordinate system. Therefore, every geometric shape within this system possesses defined coordinates and we can use Euclidean transformations to change their position and orientation is space. But sometimes, it’s cumbersome to calculate the new coordinates. Also, when we draw a shape, its generation mechanism aligns it to the world coordinate system’s axes.

To ease both, the generation and transformation of geometric objects, there are construction planes, also called reference planes. Such a plane introduces a separate, local coordinate system and can be visioned as a drawing table set anywhere in space. For example, instead of creating a box in the world coordinate system and then rotate and move it to its destined position, we can also create a reference plane and then draw the box on this plane.

A lot of components in Grasshopper let us set a reference plane for either the creation of objects, transformations, or other operations. In general, it’s a better idea to generate construction planes first and then create the objects on top of them. In an algorithm, it’s easy to generate a unique plane for every object.

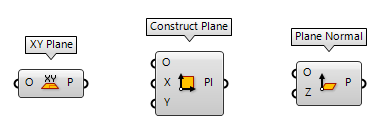
Construct planes

The ribbon group Vector > Plane hosts various components to create planes. For example: XY Planecreates a plane parallel to the world XY plane, but we can alter the origin of the coordinate system. With Construct Plane, we can set the origin and also the direction of the axes. Plane Normalcreates a plane at the provided origin and perpendicular to the vector at Z.

You can find a couple more components to create planes with various input parameters. The components are self-explanatory.

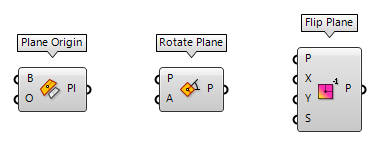
Modify planes

The desired construction plane can also be obtained by altering an existing one. The components are hosted in the same ribbon group Vector > Plane. For example, we can modify the origin of an existing plane with Plane Originor change the orientation of the axes with Rotate Plane. Flip Planeswaps the axes to our needs.

Again, there are a couple more components that do all kinds of adjustments with provided planes.

Deconstruct planes

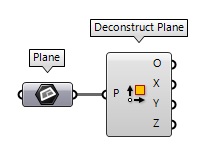
The component Deconstruct Planewill dismantle a plane into its origin and axes.

Construct planes with curves

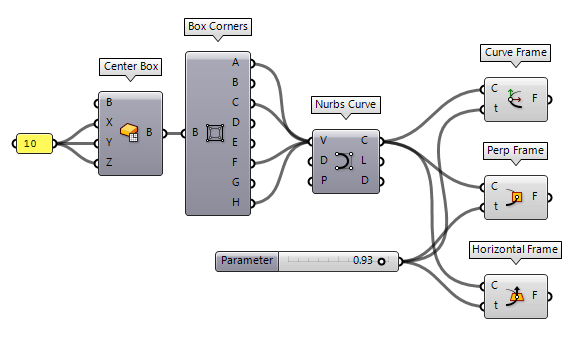
Besides vectors, we can also derive planes from curves. With given curve parameters t, there are three option: Curve Framecreates a plane in which the tangent is the x-axis, Perp Framecreates a plane in which the tangent is the z-axis and Horizontal Framecreates a plane that is parallel to the world xy plane and which has its origin at curve parameter t.

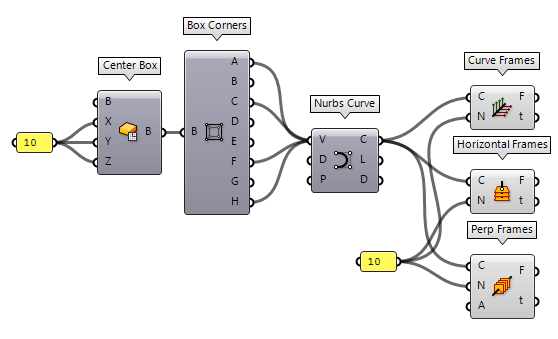
Instead of setting specific curve parameters, we can also use the related components Curve Frames, Perp Framesand Horizontal Frames. Here, we define at input N the number of segments in which the curve is divided into. The frames (planes) are created at each division point.

Retrieve local coordinates

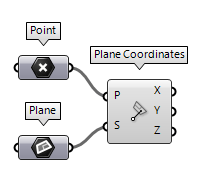
To find the local coordinates of a point on a construction plane, we can use Plane Coordinatesalong with our point P and the construction plane at S.

Retrieve planes from curves

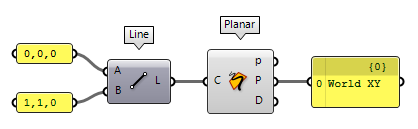
For planar curves, we can use Planarnot only to verify the curve’s planarity, but also to find the plane that the curve is in. Unlike Curve Frame, which uses a tangent of the curve to construct the plane, Planar orients the plane to the world coordinate system.

Retrieve planes from surfaces

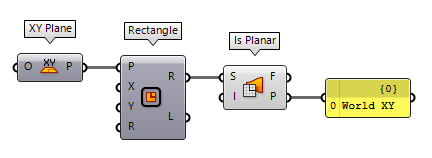
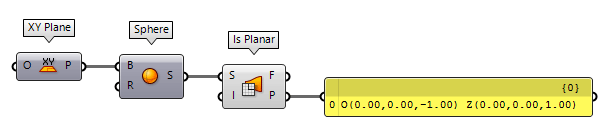
To find the plane of a planar surface, we can use Is Planarto get the verification and the surface’s plane.

Using this component with a non-planar surface will return any plane, even when the surface was constructed with a base (construction) plane.

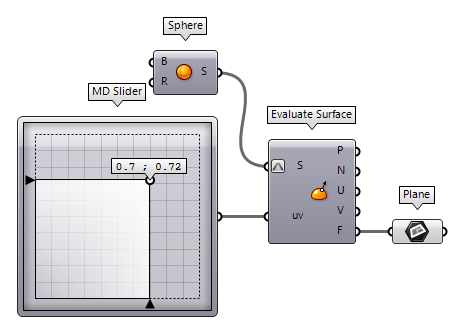
For non-planar surfaces, there is no unified plane and we need to evaluate a point on the surface to get the plane at this position. To do so, we use Evaluate Surfaceand attach uv-coordinates that match the domain of the surface.

Using Planes in Transformations

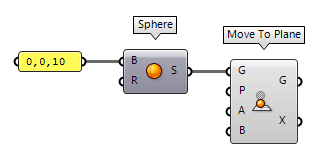
Besides the basic transformations mentioned in the beginning of this how-to, there are two powerful components to relocate geometric objects with reference planes. The first one is Move To Plane: This component takes a geometry object G and a plane P as input and moves the objects onto the provided plane. At input A and B we can set a Boolean to false if objects on one side of the plane, above (A) or below (B), should not be moved. The objects are translated until the shape touches the plane.

The other component is Orientand it resembles a move and rotate transformation. We need to provide the geometric objects G and their initial (source) planes at A. At input B we set the target plane(s). The coordinates of the object are then remapped to the new plane. This is helpful to reposition and arrange objects independent of their previous relation.